作者:老余捞鱼
原创不易,转载请标明出处及原作者。

写在前面的话:众所周知,传统的股票预测模型有着各种各样的局限性。但在我的最新研究中,探索了一些方法来高效预测股市走势,即CNN、RNN和LSTM这些深度学习模型。这种方法在揭示金融数据的复杂性和变化趋势方面取得了一些成效。在本文中,我将带大家一步步了解如何利用特斯拉股票的案例,通过这些模型进行数据预处理、模型构建、训练和预测,希望这样一个新的股市预测工具模板,能助力您的投资决策。
一、股票价格预测方法的问题与发展
股票市场,尤其是股票价格预测,是一个备受研究人员和从业人员关注的领域。传统的时间序列预测方法,如自回归(AR)、自回归移动平均(ARMA)和自回归综合移动平均(ARIMA)模型在这方面发挥了重要作用。这些方法依赖于预定义的数学公式来模拟单变量时间序列,由于其简单性和可解释性而被广泛接受。
然而,AR、ARMA 和 ARIMA 有其固有的局限性,因此不适合捕捉金融时间序列数据的潜在动态特征。其中一个限制是,为一个时间序列确定的模型不能很好地推广到其他时间序列,从而降低了其通用性。此外,这些模型难以识别数据中蕴含的复杂模式,限制了其有效性。
近年来,卷积神经网络(CNN)、循环神经网络(RNN)等先进的机器学习模型及其变体(如长短期记忆(LSTM))引起了广泛关注。这些模型利用其从历史数据中学习的能力,不需要预定义的方程式,因此非常适合揭示隐藏的关系和依赖性。它们将金融数据建模为多维问题,从而实现了更准确、更稳健的预测。
本文将探讨 CNN、RNN 和基于注意力的 LSTM 在预测特斯拉股票价格中的应用。目的是展示每种方法的优缺点,并深入探讨深度学习模型如何超越传统线性模型。
二、为什么选择特斯拉股票?
特斯拉公司 (TSLA) 是最吸引分析师和投资者的股票之一,是评估 LSTM、RNN 和 CNN 等高级预测模型性能的理想选择。该公司是高风险、高回报投资的代表,因其技术创新以及围绕其领导地位和市场动态的争议而备受关注。
该公司创始人埃隆-马斯克(Elon Musk)是科技行业中最两极分化的人物之一,他一直在推动对特斯拉业绩的猜测。他支持唐纳德-特朗普总统参加 2024 年美国大选,进一步加剧了不确定性,加剧了该股的波动性,如下图所示。
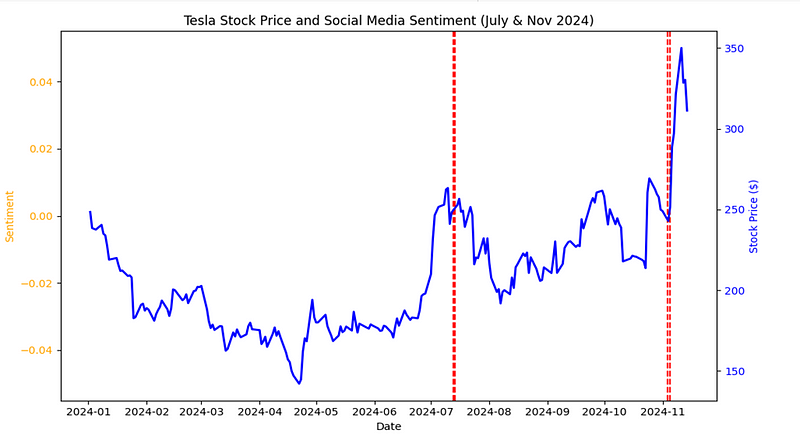
这种猜测水平加上马斯克的公众形象,凸显了特斯拉作为旨在捕捉动态嘈杂数据的模型试验场的潜力。从 2010 年到 2024 年的收盘价就说明了这一点。

三、数据准备
3.1 数据收集
我们使用 yfinance 库中的特斯拉历史股价数据。
import yfinance as yf
import pandas as pd
def fetch_tesla_stock_data():
"""
Fetch Tesla's historical stock data from Yahoo Finance.
Returns:
pd.DataFrame: DataFrame containing adjusted close prices indexed by date.
"""
# Fetch data for Tesla (TSLA) from Yahoo Finance
ticker = "TSLA"
start_date = "2010-01-01"
end_date = "2024-11-17"
tesla = yf.download(ticker, start=start_date, end=end_date)
# Return a DataFrame with the adjusted close prices
tesla_data = tesla[['Adj Close']].rename(columns={"Adj Close": "adjClose"})
tesla_data.index.name = "date"
return tesla_data
# Fetch Tesla stock data
tesla_data = fetch_tesla_stock_data()
# Display the first few rows of data
print(tesla_data.head(10))3.2 数据预处理
开发一个预处理管道,首先使用 MinMaxScaler 对特斯拉调整后的收盘价进行归一化处理。这一步骤可确保模型能有效处理数据,而不会受到原始值规模的影响。我们还使用滑动窗口创建历史股票价格序列。每个滑动窗口跨越 20 天(窗口大小)。最后,我们将数据重塑为适合 LSTM、RNN 和 CNN 的格式。重要的是,我们不对训练和测试数据进行洗牌,以保留股票价格的时间顺序。
import numpy as np
import pandas as pd
from sklearn.preprocessing import MinMaxScaler
from sklearn.metrics import mean_absolute_percentage_error
from sklearn.model_selection import train_test_split
# Define the window size and prediction time
window_size = 20
prediction_steps = 10
# Function to create sequences
def create_sequences(data, window_size, prediction_steps):
X = []
y = []
for i in range(window_size, len(data) - prediction_steps):
X.append(data[i-window_size:i, 0]) # input sequence
y.append(data[i+prediction_steps-1, 0]) # target value (price at the next timestep)
return np.array(X), np.array(y)
# Fetch Tesla stock data
data = tesla_data[['adjClose']].values
# Normalize the data using MinMaxScaler
scaler = MinMaxScaler(feature_range=(0, 1))
scaled_data = scaler.fit_transform(data)
# Create sequences for the model
X, y = create_sequences(scaled_data, window_size, prediction_steps)
# Reshape input data to be in the shape [samples, time steps, features]
X = X.reshape(X.shape[0], X.shape[1], 1)
# Split the data into training and testing sets
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, shuffle=False)
print(f"Training data shape: {X_train.shape}")
print(f"Testing data shape: {X_test.shape}")四、使用模型进行预测
4.1 使用 LSTM 预测
该模型包含一个自定义注意力层,以增强其捕捉特斯拉股票价格中关键时间模式的能力。该模型由 50 个单元组成,用于预处理输入序列,并通过内部记忆机制保留重要的时间依赖性。我们还加入了一个剔除层,通过在训练过程中随机禁用神经元来降低过度拟合的风险。训练结束后,我们将测试模型的性能,并绘制其预测结果与实际股票价格的对比图。
import numpy as np
import tensorflow as tf
from keras.models import Sequential
from keras.layers import LSTM, Dense, Dropout, Attention, Add, LayerNormalization, Layer
from keras.callbacks import EarlyStopping
from sklearn.preprocessing import MinMaxScaler
from sklearn.metrics import mean_absolute_percentage_error
# Define a custom attention layer
class AttentionLayer(Layer):
def __init__(self, **kwargs):
super(AttentionLayer, self).__init__(**kwargs)
def build(self, input_shape):
self.W = self.add_weight(shape=(input_shape[2], input_shape[2]), initializer='random_normal', trainable=True)
self.b = self.add_weight(shape=(input_shape[1],), initializer='zeros', trainable=True)
super(AttentionLayer, self).build(input_shape)
def call(self, inputs):
q = tf.matmul(inputs, self.W)
a = tf.matmul(q, inputs, transpose_b=True)
attention_weights = tf.nn.softmax(a, axis=-1)
return tf.matmul(attention_weights, inputs)
# LSTM model with attention and early stopping
def build_lstm_model_with_attention(input_shape):
model = Sequential()
model.add(LSTM(units=50, return_sequences=True, input_shape=input_shape))
model.add(Dropout(0.2))
# Attention layer
model.add(AttentionLayer())
model.add(LayerNormalization())
model.add(LSTM(units=50, return_sequences=False))
model.add(Dropout(0.2))
model.add(Dense(units=1)) # Output layer for prediction
model.compile(optimizer='adam', loss='mean_squared_error')
return model
# Build the LSTM model with attention
model = build_lstm_model_with_attention(X_train.shape[1:])
# Implement EarlyStopping to prevent overfitting
early_stopping = EarlyStopping(monitor='val_loss', patience=10, restore_best_weights=True)
# Train the model with EarlyStopping and 50 epochs
history = model.fit(X_train, y_train, epochs=70, batch_size=32, validation_data=(X_test, y_test), callbacks=[early_stopping])
# Evaluate the model
predicted_stock_price = model.predict(X_test)
predicted_stock_price = scaler.inverse_transform(predicted_stock_price)
# Inverse scale the actual stock prices
y_test_scaled = scaler.inverse_transform(y_test.reshape(-1, 1))
# Calculate MAPE
mape = mean_absolute_percentage_error(y_test_scaled, predicted_stock_price)
print(f"Mean Absolute Percentage Error (MAPE): {mape:.2f}%")
# Plot the results
plt.figure(figsize=(10, 6))
plt.plot(y_test_scaled, label="Actual Tesla Stock Price", color='blue')
plt.plot(predicted_stock_price, label="Predicted Tesla Stock Price", color='red')
plt.title('Tesla Stock Price Prediction with LSTM', fontsize=14)
plt.xlabel('Time', fontsize=12)
plt.ylabel('Scaled Stock Price (USD)', fontsize=12)
plt.legend()
plt.grid(True)
plt.show()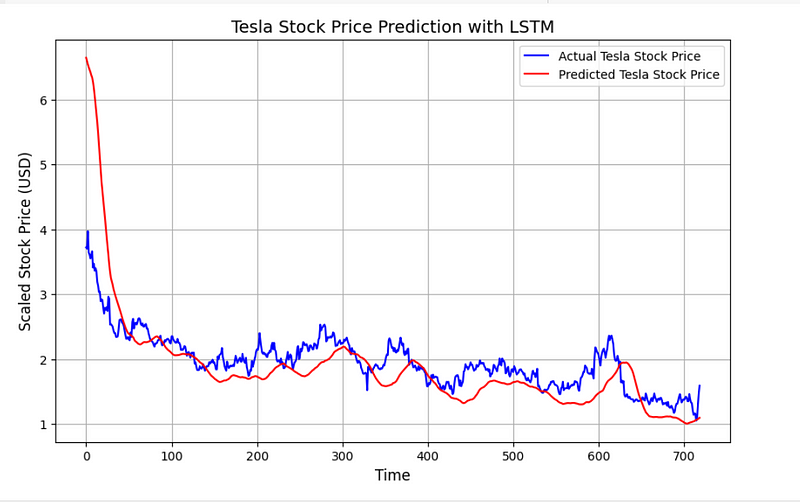
该模型从数值上看良好,平均百分比误差为 0.17%。
4.2 使用 RNN(递归神经网络)预测
LSTM 在处理顺序数据方面表现相当出色。然后,我们整合了一个 RNN,以检验它是否能捕捉时间依赖性。此外,我们还使用双向 RNN 来考虑过去和未来的输入。
from keras.models import Sequential
from keras.layers import SimpleRNN, Dense, Dropout
# Define the RNN model
def build_rnn_model(input_shape):
model = Sequential()
model.add(SimpleRNN(units=50, return_sequences=True, input_shape=input_shape))
model.add(Dropout(0.2))
model.add(SimpleRNN(units=50, return_sequences=False))
model.add(Dropout(0.2))
model.add(Dense(units=1)) # Output layer for prediction
model.compile(optimizer='adam', loss='mean_squared_error')
return model
# Build the RNN model
rnn_model = build_rnn_model(X_train.shape[1:])
# Train the model
rnn_history = rnn_model.fit(X_train, y_train, epochs=70, batch_size=32, validation_data=(X_test, y_test))
# Evaluate the model
predicted_stock_price_rnn = rnn_model.predict(X_test)
predicted_stock_price_rnn = scaler.inverse_transform(predicted_stock_price_rnn)
# Inverse scale the actual stock prices
y_test_scaled = scaler.inverse_transform(y_test.reshape(-1, 1))
# Calculate MAPE for RNN
mape_rnn = mean_absolute_percentage_error(y_test_scaled, predicted_stock_price_rnn)
print(f"Mean Absolute Percentage Error (MAPE) for RNN: {mape_rnn:.2f}%")
# Plot the results for RNN model
plt.figure(figsize=(12, 6))
plt.plot(y_test_scaled, label="Actual Tesla Stock Price", color='blue')
plt.plot(predicted_stock_price_rnn, label="Predicted Tesla Stock Price", color='red')
plt.title('Tesla Stock Price Prediction with RNN', fontsize=14)
plt.xlabel('Time', fontsize=12)
plt.ylabel(' Scaled Stock Price (USD)', fontsize=12)
plt.legend()
plt.grid(True)
plt.show()下图是RNN 的预测结果:
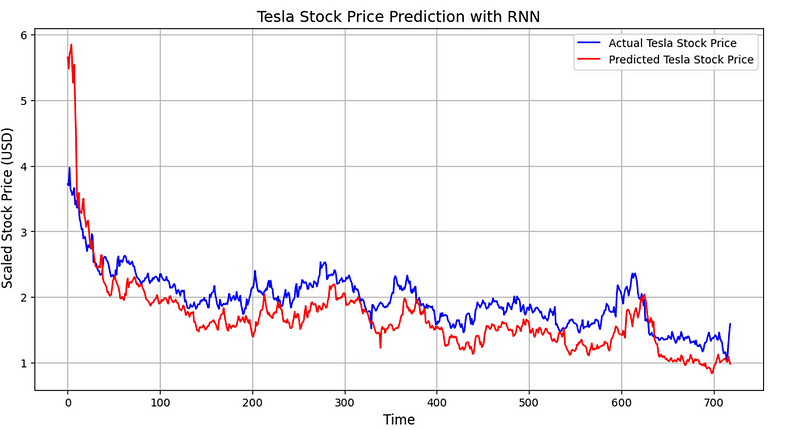
这是 LSTM 与 RNN的比较图:
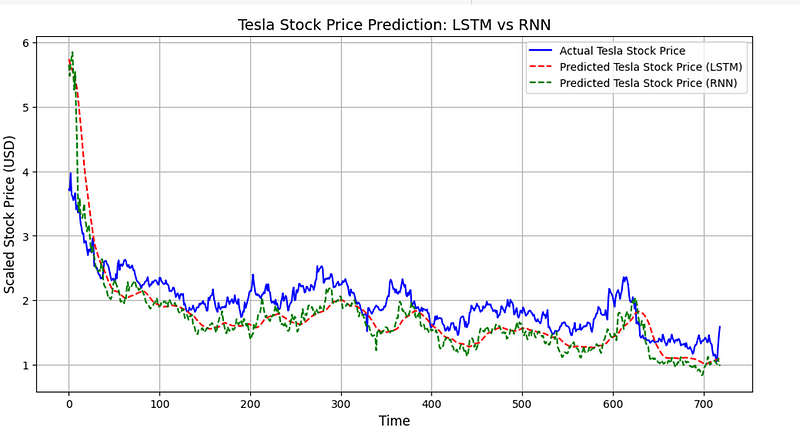
如图所示, RNN 模型的平均绝对百分比误差和 LSTM 相近。
4.3 使用 CNN(卷积神经网络)预测
最后,我们使用 CNN 来研究它在预测特斯拉股价方面的表现。该模型的结构是自动学习数据中的空间层次和模式。我们应用了多个卷积层,使用过滤器来检测输入数据中的重要特征。此外,我们还使用池化层来降低特征图的维度,并保留最重要的信息。由于我们使用全连接层,因此输出是预测未来股价的回归值。
from keras.models import Sequential
from keras.layers import Conv1D, MaxPooling1D, Flatten, Dense, Dropout, BatchNormalization
from keras.callbacks import EarlyStopping,ReduceLROnPlateau
from sklearn.metrics import mean_absolute_percentage_error
from sklearn.preprocessing import MinMaxScaler
from sklearn.model_selection import train_test_split
def build_cnn_model(input_shape):
model = Sequential()
model.add(Conv1D(filters=64, kernel_size=3, activation='relu', input_shape=input_shape))
model.add(BatchNormalization())
model.add(MaxPooling1D(pool_size=2))
model.add(Conv1D(filters=64, kernel_size=3, activation='relu'))
model.add(BatchNormalization())
# Change pool_size to avoid reducing dimensions to zero
model.add(MaxPooling1D(pool_size=2))
# Add a condition to avoid further reduction if dimensions are too small
model.add(Conv1D(filters=64, kernel_size=3, activation='relu'))
model.add(BatchNormalization())
model.add(MaxPooling1D(pool_size=1)) # Adjusted pool size
model.add(Flatten())
model.add(Dropout(0.4))
model.add(Dense(units=100, activation='relu'))
model.add(Dropout(0.2))
model.add(Dense(units=1)) # Output layer for prediction
model.compile(optimizer='adam', loss='mean_squared_error')
return model
cnn_model = build_cnn_model(X_train.shape[1:])
early_stopping = EarlyStopping(monitor='val_loss', patience=30, restore_best_weights=True)
reduce_lr = ReduceLROnPlateau(monitor='val_loss', factor=0.5, patience=10, min_lr=1e-6)
cnn_history = cnn_model.fit(
X_train, y_train,
epochs=200,
batch_size=32,
validation_data=(X_test, y_test),
callbacks=[early_stopping, reduce_lr]
)
# Build the CNN model
cnn_model = build_cnn_model(X_train.shape[1:])
# Define EarlyStopping callback
early_stopping = EarlyStopping(monitor='val_loss', patience=30, restore_best_weights=True)
# Train the model with early stopping and 100 epochs
cnn_history = cnn_model.fit(X_train, y_train, epochs=100, batch_size=32, validation_data=(X_test, y_test), callbacks=[early_stopping])
# Evaluate the model
predicted_stock_price_cnn = cnn_model.predict(X_test)
predicted_stock_price_cnn = scaler.inverse_transform(predicted_stock_price_cnn)
# Inverse scale the actual stock prices
y_test_scaled = scaler.inverse_transform(y_test.reshape(-1, 1))
# Calculate MAPE for CNN
mape_cnn = mean_absolute_percentage_error(y_test_scaled, predicted_stock_price_cnn)
print(f"Mean Absolute Percentage Error (MAPE) for CNN: {mape_cnn:.2f}%")
# Plot the results for CNN model
plt.figure(figsize=(12, 6))
plt.plot(y_test_scaled, label="Actual Tesla Stock Price", color='blue')
plt.plot(predicted_stock_price_cnn, label="Predicted Tesla Stock Price (CNN)", color='red')
plt.title('Tesla Stock Price Prediction with CNN', fontsize=14)
plt.xlabel('Time', fontsize=12)
plt.ylabel('Scaled Stock Price (USD)', fontsize=12)
plt.legend()
plt.grid(True)
plt.show()下图是 CNN 的预测结果:
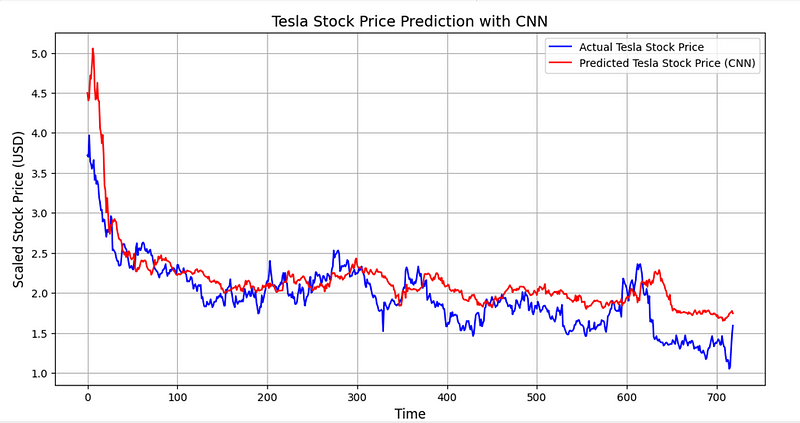
这是 CNN 与LSTM 、RNN的比较图:
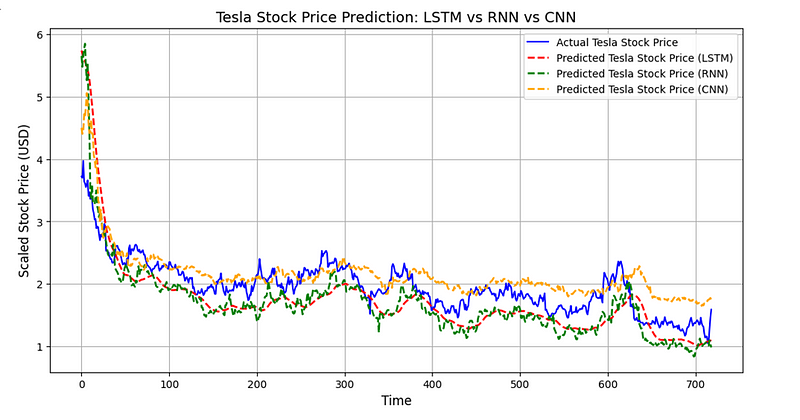
CNN 模型的平均绝对百分比误差为 0.14%,优于 LSTM 和 RNN。
4.4 比较结果
三种模型的平均绝对误差百分比如下:
import matplotlib.pyplot as plt
mape_scores = [mape, mape_rnn, mape_cnn]
models = ['LSTM', 'RNN', 'CNN']
# Create the bar chart
plt.figure(figsize=(6, 4))
plt.bar(models, mape_scores, color=['blue', 'green', 'orange'])
# Add labels and title
plt.title('MAPE Comparison for LSTM, RNN, and CNN', fontsize=14)
plt.xlabel('Models', fontsize=12)
plt.ylabel('MAPE (%)', fontsize=12)
# Show the MAPE values on top of the bars
for i, v in enumerate(mape_scores):
plt.text(i, v + 0.1, f'{v:.2f}%', fontsize=12)
# Display the plot
plt.show()性能比较图如下:
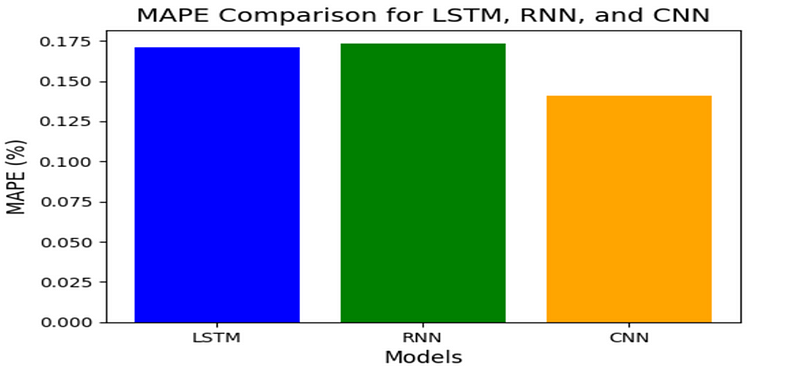
基于深度学习的股票预测方法采用三种不同的神经架构,能够很好地捕捉隐藏的动态变化。虽然特斯拉股票波动性很大,但我们的模型实现了非常低的平均绝对百分比误差(MAPE):LSTM和RNN 都是 0.17%,CNN 为 0.14%。
这证明了深度学习模型能有效捕捉时间差和隐藏模式,而 CNN 能有效捕捉股票价格的突然变化和趋势。
五、观点总结
- 传统时间序列预测模型存在局限性:AR、ARMA 和 ARIMA 等传统模型在金融数据的预测中表现出模型泛化能力差和难以捕捉复杂模式的问题。
- 深度学习模型在股票预测中的优势:CNN、RNN 和 LSTM 等深度学习模型能够从历史数据中自动学习,无需预设的数学方程,更适合处理金融时间序列数据的复杂性。
- 特斯拉股票的特殊性:特斯拉股票的高波动性和与其相关的公众关注度,使其成为测试股票预测模型的理想案例。
- 模型性能比较:通过对比 LSTM、RNN 和 CNN 模型在特斯拉股票预测上的表现,得出 CNN 模型在本次实验中具有最佳的预测能力。
精选10篇和股票预测相关的文章推荐:
- 仅需八步,打造私人专属智能股票预测模型
- 手把手教会你用 AI 和 Python 进行股票交易预测(完整代码干货)
- 揭秘:如何用思想增强型LSTM网络精准预测股价?
- 震惊金融界!三大深度学习模型联袂,竟创出66,941.5%逆天回报率!
- 美国大选后,用HMM模型做特斯拉股价波动解析
- 使用堆叠 LSTM 模型预测市场趋势
- 获得简街市场预测大赛金牌的预测策略模型
- 融合篇:用 OpenAI o1 草莓模型和 Python 预测股市行情
- 【Python时序预测系列】基于LSTM实现多输入多输出单步预测(案例+源码)
- 用 Python 中的量子机器学习预测股票价格
谢谢您阅读到最后,希望本文能给您带来新的收获。祝您投资顺利!如果对文中的内容有任何疑问,请给我留言,必复。
本文内容仅限技术探讨和学习,不构成任何投资建议。