推导LSTM网络中参数的梯度, 并分析其避免梯度消失的效果
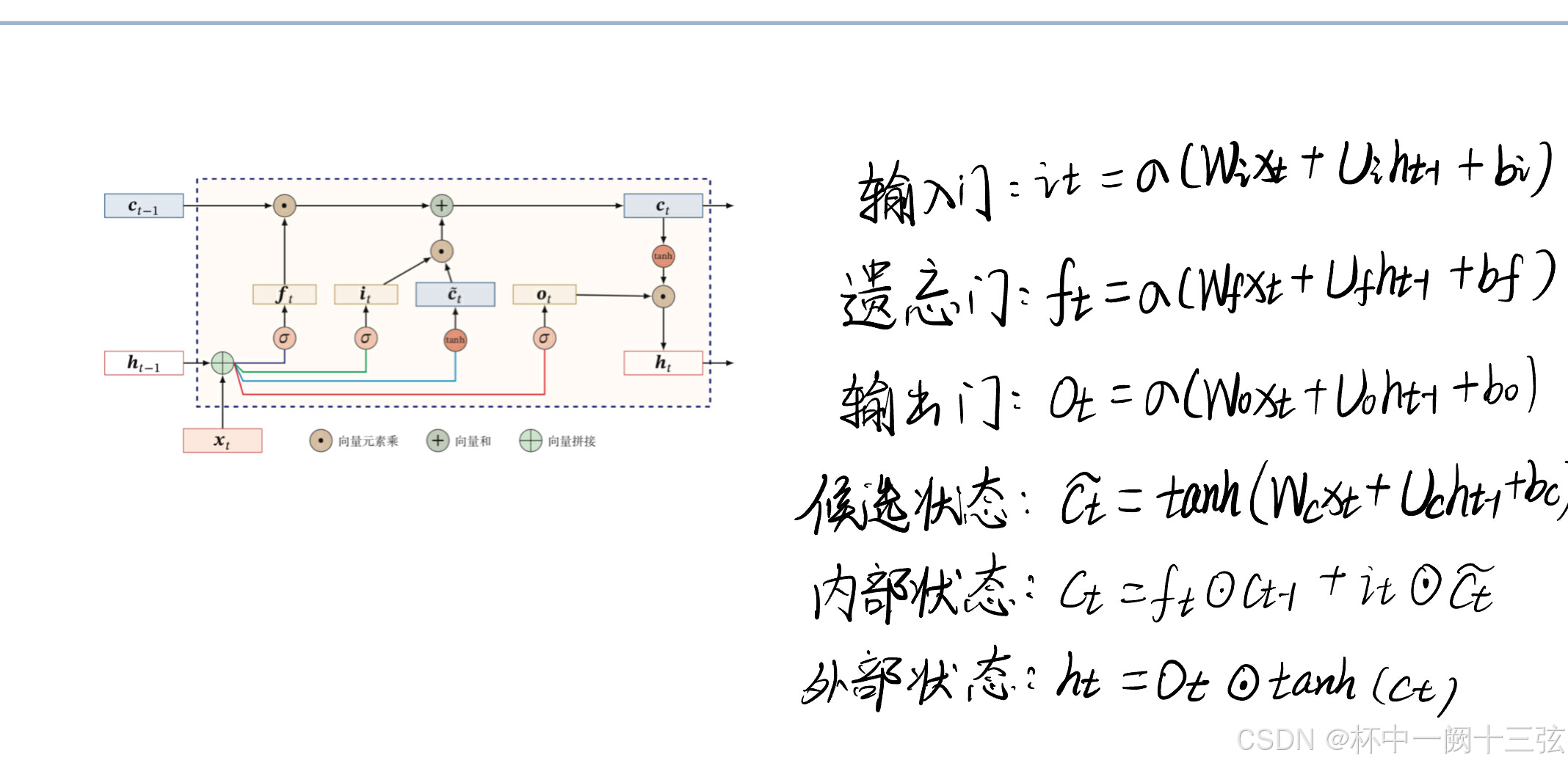
根据LSTM的计算公式,可以得出LSTM的cell state与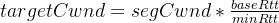 、
、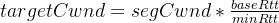 、
、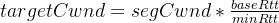 都存在计算关系,而
都存在计算关系,而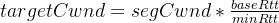 、
、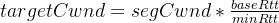 、
、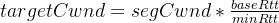 的计算公式又全部都与
的计算公式又全部都与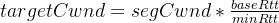 有关,所以从
有关,所以从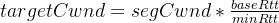 到
到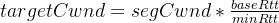 的反向传播的公式如下:
的反向传播的公式如下:
由LSTM各个门的计算公式可以进一步推导得到:
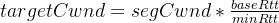
根据公式,如果要计算时刻k的,简单的利用上式进行乘t-k+1次即可。在公式中的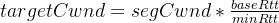 ,也就是遗忘门
,也就是遗忘门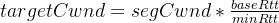 可以控制的值。由于
可以控制的值。由于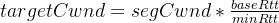 的值也与
的值也与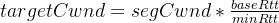 前面三项值有关,所以
前面三项值有关,所以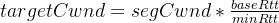 的值不一定局限于[0,1],也有可能是大于1的,所以在一定程度上减缓了梯度消失。从计算公式角度来看
的值不一定局限于[0,1],也有可能是大于1的,所以在一定程度上减缓了梯度消失。从计算公式角度来看 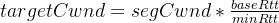 、
、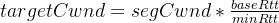 、
、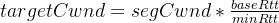 与
与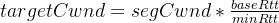 都是LSTM学习得到的,LSTM会通过学习改变门控的值来决定什么时候遗忘梯度,什么时候保留梯度,即依靠学习得到权值去控制依赖的长度。
都是LSTM学习得到的,LSTM会通过学习改变门控的值来决定什么时候遗忘梯度,什么时候保留梯度,即依靠学习得到权值去控制依赖的长度。
那么什么情况下大于1?
这个由LSTM自身的权值决定,那权值从何而来?当然是学习得到的,这便是LSTM牛逼之处,依靠学习得到权值去控制依赖的长度,这便是LSTM缓解梯度消失的真相。综上可以总结为两个事实:
1、cell state传播函数中的“加法”结构确实起了一定作用,它使得导数有可能大于1;
2、LSTM中逻辑门的参数可以一定程度控制不同时间步梯度消失的程度。
LSTM依然不能完全解决梯度消失这个问题,有文献表示序列长度一般到了三百多仍然会出现梯度消失现象。如果想彻底规避这个问题,还是transformer好用。
在推导 LSTM 网络中其他参数的梯度时,运用链式法则展开后会发现,梯度在更新过程中会乘以一个常数系数(也就是导数)。这个特性有着重要意义,因为在传统的循环神经网络(RNN)中,反向传播时梯度是连乘的形式,随着序列长度增加,连乘的梯度项容易变得极小,进而导致梯度消失问题。而 LSTM 中这种乘以常数系数的情况,改变了梯度的传播方式,避免了像传统 RNN 那样梯度快速衰减直至消失的情况出现,从而有助于应对梯度消失问题。
遗忘门、输入门和输出门之间的运算关系(在细胞状态和隐藏状态的更新公式中是非 0 即 1,且多为相加关系),为梯度在 LSTM 网络中的良好传递创造了条件。当某个门为 0 时,意味着对应的信息流动通道被阻断,比如遗忘门为 0 时,上一时刻的信息对当前时刻就没有影响了,也就没必要接受其传递来更新参数了,从这个角度看,这种机制可以精准地控制信息和梯度的传递路径,减轻了梯度消失发生的概率,让梯度能够更顺畅、合理地在网络各时间步之间传递,保障网络在处理长序列数据时能更有效地学习和更新参数。
上面是跟着CSDN上某位博主的思路串下来的,然后我又听说B站上有位大神讲的不错
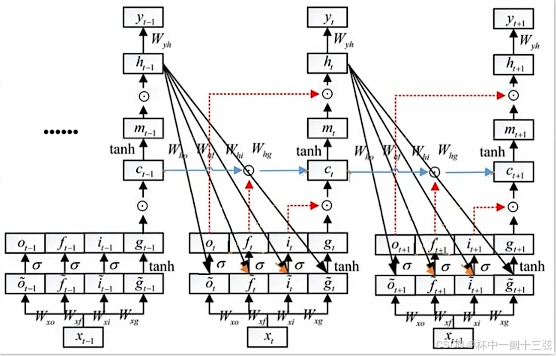
第一次看到这个图,差点把中午饭呕出来
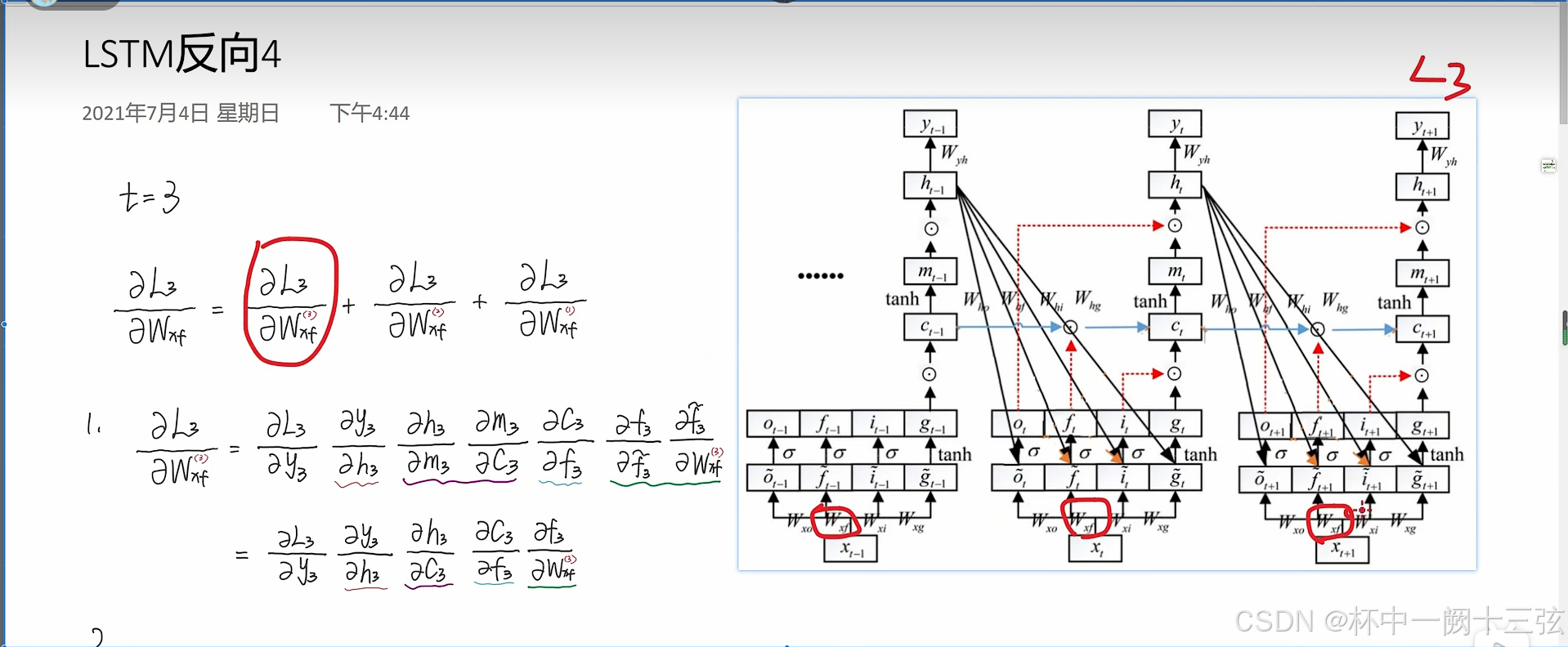
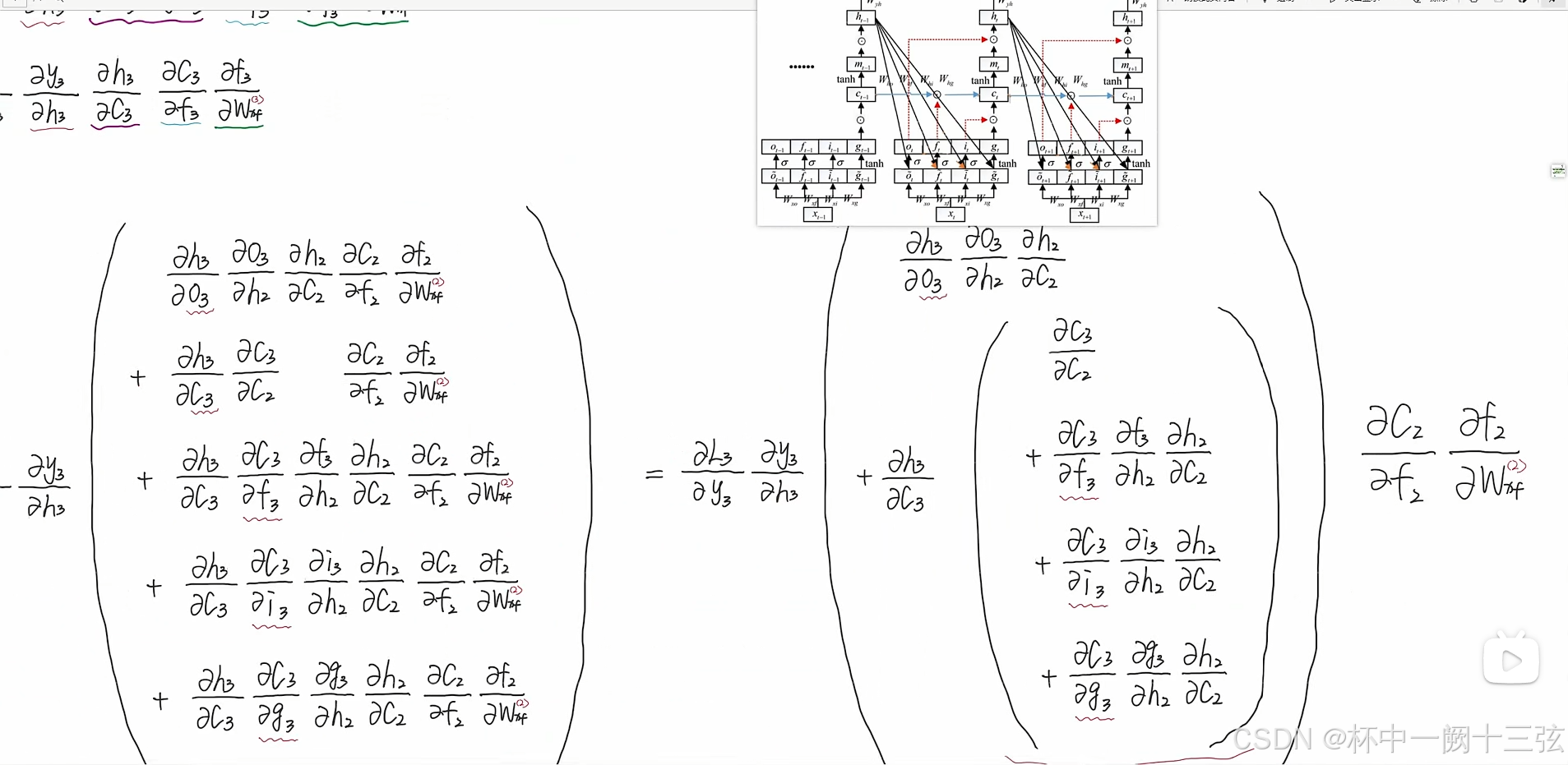
这位博主的思路就是把跟参数有关的所有的路径找出来,再一条条求
排列组合,每往前进一个,路径就会增加很多
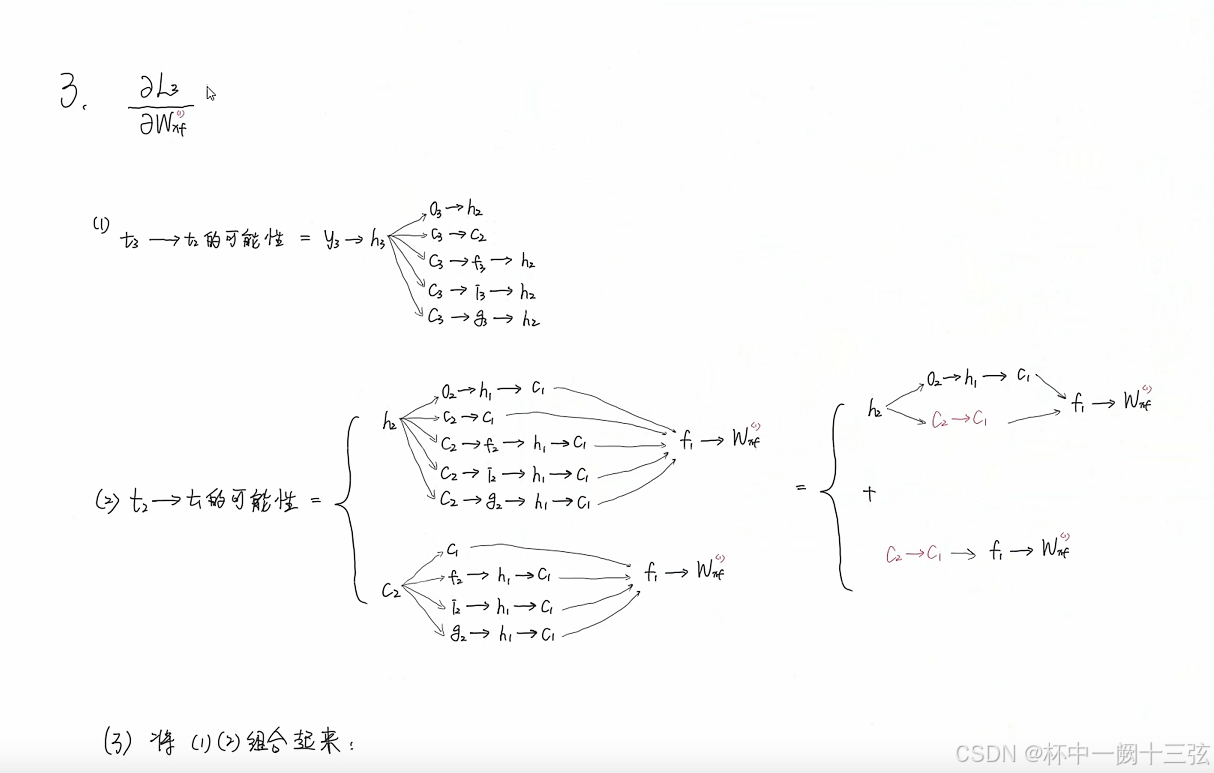
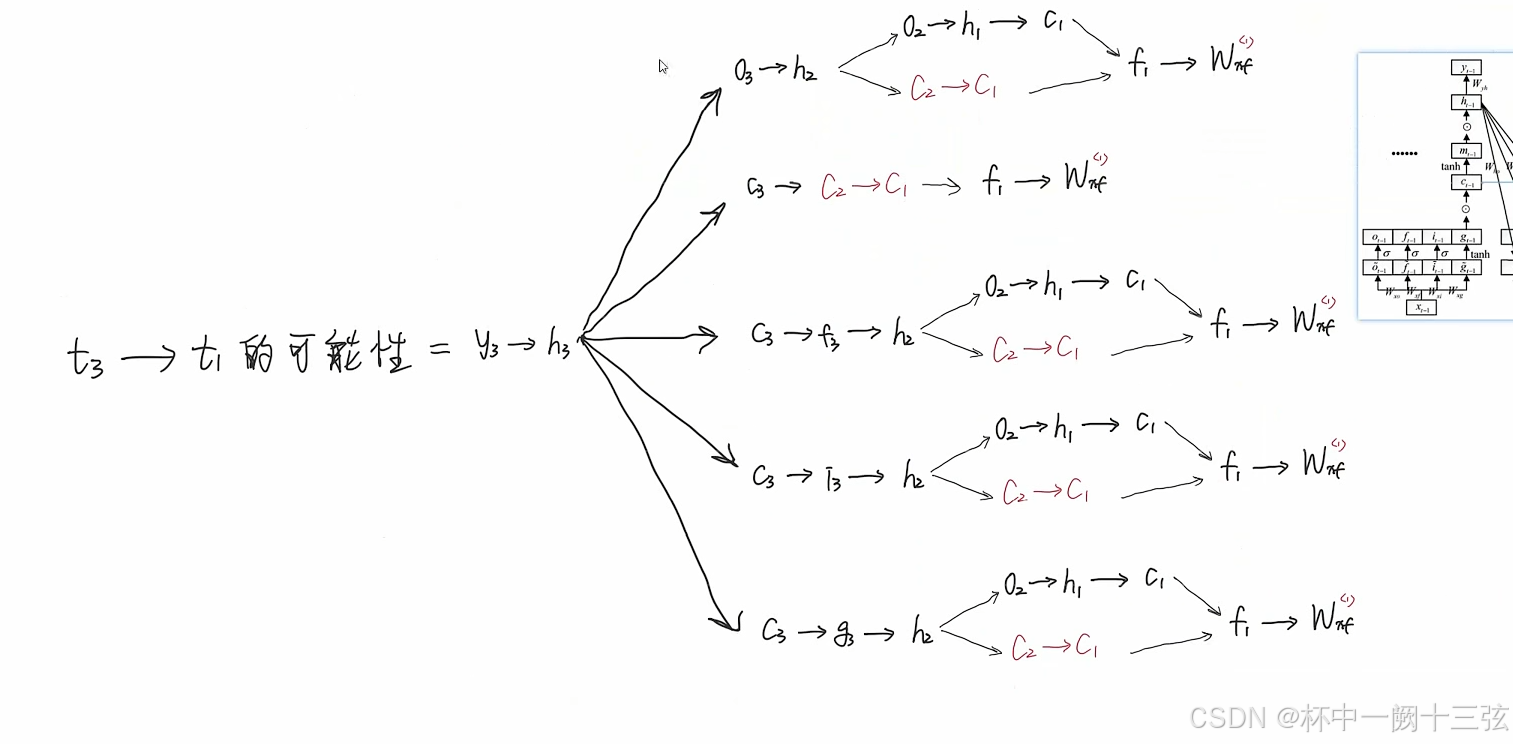
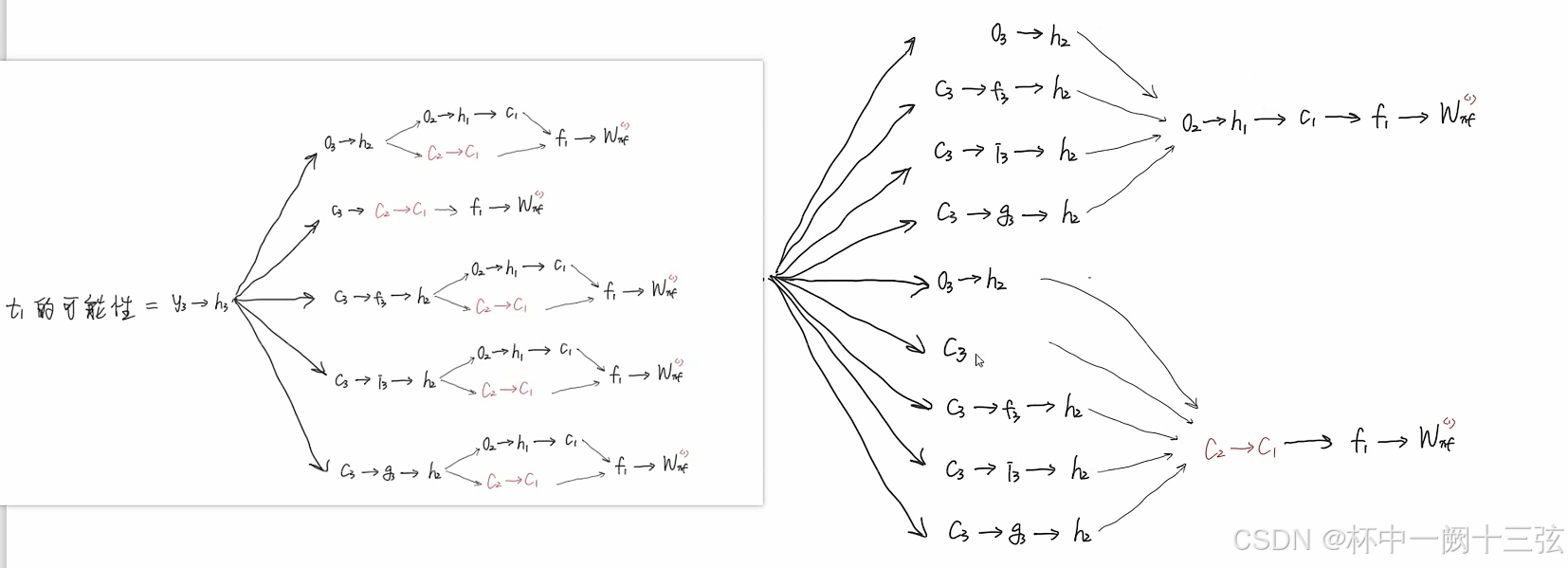
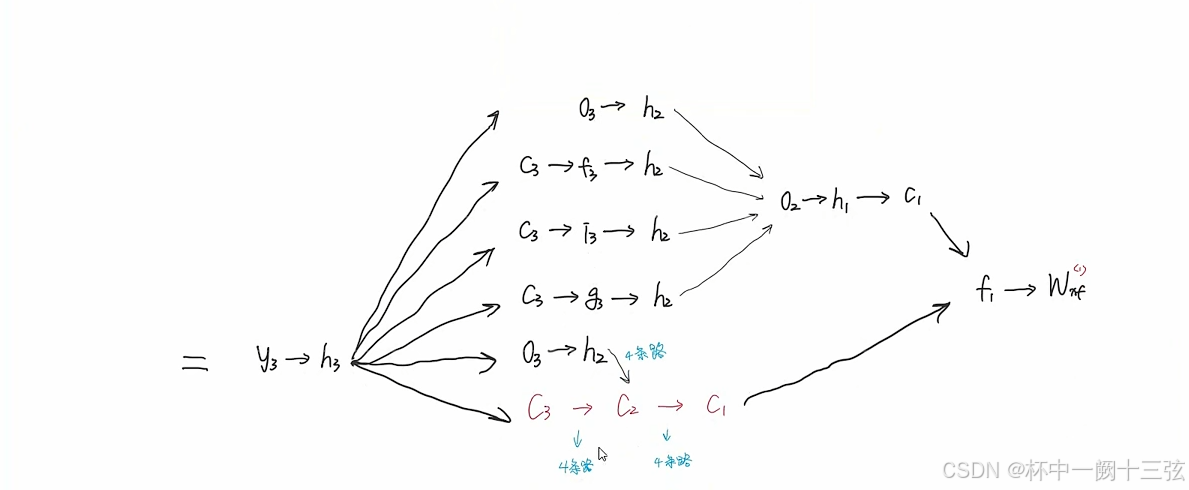
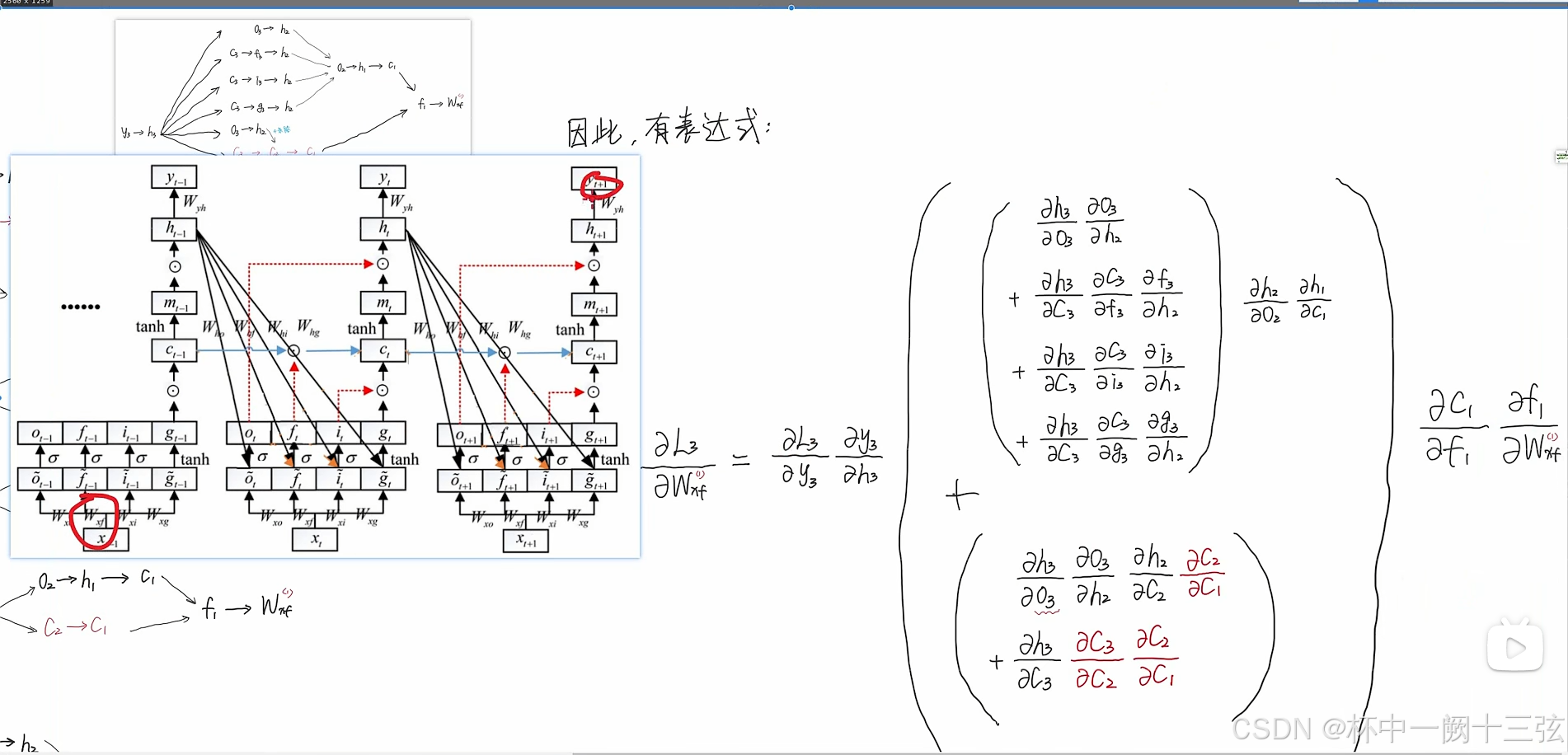

编程实现下图LSTM运行过程
1、使用Numpy实现LSTM算子
2、使用nn.LSTMCell实现
3、使用nn.LSTM实现

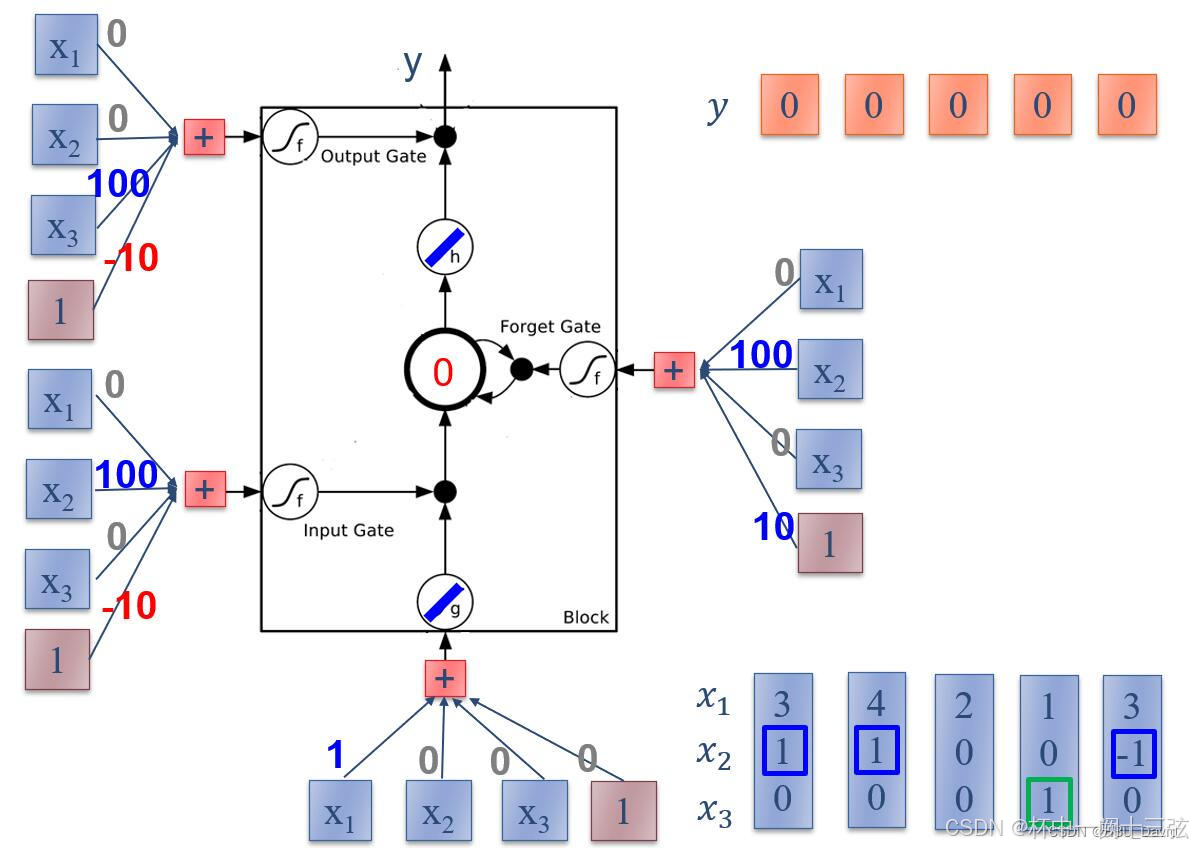
# numpy算子实现LSTM
import numpy as np
# 初始化输入序列,每行代表一个时间步的输入 [x1 x2 x3 label]
x = np.array([[1, 0, 0, 1],
[3, 1, 0, 1],
[2, 0, 0, 1],
[4, 1, 0, 1],
[2, 0, 0, 1],
[1, 0, 1, 1],
[3, -1, 0, 1],
[6, 1, 0, 1],
[1, 0, 1, 1]])
# 权重初始化
c_W = np.array([1, 0, 0, 0]) # 细胞状态权重
inputGate_W = np.array([0, 100, 0, -10]) # 输入门权重
outputGate_W = np.array([0, 0, 100, -10]) # 输出门权重
forgetGate_W = np.array([0, 100, 0, 10]) # 遗忘门权重
# sigmoid函数 用于LSTM中各种门的操作
def sigmoid(x):
y = 1 / (1 + np.exp(-x))
if y >= 0.5:
return 1
else:
return 0
temp = 0
y = []
c = []
for input in x:
c.append(temp) # 保存上一时刻的细胞状态
temp_c = np.sum(np.multiply(input, c_W)) # 新细胞状态的线性组合
# 输入门 遗忘门 输出门
# multiply表示点乘运算 sigmoid将数值进行非线性变换
temp_input = sigmoid(np.sum(np.multiply(input, inputGate_W)))
temp_forget = sigmoid(np.sum(np.multiply(input, forgetGate_W)))
temp_output = sigmoid(np.sum(np.multiply(input, outputGate_W)))
temp = temp_c * temp_input + temp_forget * temp # 更新细胞状态
y.append(temp_output * temp) # 通过输出门得到输出,保存下来
print("Memory:", c)
print("Y :", y)
import torch
import torch.nn as nn
# 输入数据 x 维度需要变换,因为LSTMcell接收的是(time_steps,batch_size,input_size)
x = torch.tensor([[1, 0, 0, 1],
[3, 1, 0, 1],
[2, 0, 0, 1],
[4, 1, 0, 1],
[2, 0, 0, 1],
[1, 0, 1, 1],
[3, -1, 0, 1],
[6, 1, 0, 1],
[1, 0, 1, 1]], dtype=torch.float)
# 增加1个batch维度,x由原来的3*4的矩阵变为3*1*4的张量
x = x.unsqueeze(1)
hidden_size = 1
# 使用LSTMCell定义LSTM单元
lstm_cell = nn.LSTMCell(input_size=4, hidden_size=1, bias=False)
lstm_cell.weight_ih.data = torch.tensor([[0, 100, 0, 10], # forget gate
[0, 100, 0, -10], # input gate
[1, 0, 0, 0], # output gate
[0, 0, 100, -10]]).float() # cell gate
lstm_cell.weight_hh.data = torch.zeros([4 * hidden_size, hidden_size])
# https://runebook.dev/zh/docs/pytorch/generated/torch.nn.lstmcell
# 初始化隐藏状态和细胞状态 初始值设为0
hx = torch.zeros(1, hidden_size)
cx = torch.zeros(1, hidden_size)
outputs = []
for i in range(len(x)):
hx, cx = lstm_cell(x[i], (hx, cx)) # 前向传播
outputs.append(hx.detach().numpy()[0][0]) # .detach()方法为确保tensor不计算梯度
outputs_rounded = [round(x) for x in outputs] # 四舍五入到最接近的整数
print(outputs_rounded)
import torch
import torch.nn as nn
# 输入数据 x 维度需要变换,因为 LSTM 接收的是 (sequence_length, batch_size, input_size)
x = torch.tensor([[1, 0, 0, 1],
[3, 1, 0, 1],
[2, 0, 0, 1],
[4, 1, 0, 1],
[2, 0, 0, 1],
[1, 0, 1, 1],
[3, -1, 0, 1],
[6, 1, 0, 1],
[1, 0, 1, 1]], dtype=torch.float)
# 增加1个batch维度,x由原来的3*4的矩阵变为3*1*4的张量
x = x.unsqueeze(1)
# 输入size 和 隐藏状态 size
input_size = 4
hidden_size = 1
# 定义LSTM模型
lstm = nn.LSTM(input_size=input_size, hidden_size=hidden_size, bias=False)
# 设置权重矩阵
# 只设置了输入到隐藏层的权重,而隐藏层到隐藏层的权重被设置为零。
lstm.weight_ih_l0.data = torch.tensor([[0, 100, 0, 10], # forget gate
[0, 100, 0, -10], # input gate
[1, 0, 0, 0], # output gate
[0, 0, 100, -10]]).float() # cell gate
# 隐藏层到隐藏层的权重设置为零
lstm.weight_hh_l0.data = torch.zeros([4 * hidden_size, hidden_size])
# 初始化隐藏状态和记忆状态
hx = torch.zeros(1, 1, hidden_size)
cx = torch.zeros(1, 1, hidden_size)
# 前向传播
outputs, (hx, cx) = lstm(x, (hx, cx))
# 通过.squeeze()方法去掉batch维度,得到一个一维的输出结果
outputs = outputs.squeeze().tolist()
# 四舍五入到最接近的整数
outputs_rounded = [round(x) for x in outputs]
print(outputs_rounded)
结果,和使用nn.LSTMCell()构建的结果一样。
参考链接:
【神经网络】LSTM为什么能缓解梯度消失_lstm如何克服梯度消失-CSDN博客
LSTM网络参数梯度推导与解决梯度消失策略 (csdn.net)