文章目录
前言
按照傅里叶发展的历史,本应该先介绍傅里叶级数,但是由于DTFT更通用,且DTFT是属于核心理论,而DFS是DTFT的一种特列,所以该系列文章中先介绍DTFT,也就是离散时间傅里叶变换。
|版本声明:山河君,未经博主允许,禁止转载
一、DTFT的解释
1.DTFT公式
看一下DTFT和CFT也就是连续傅里叶变换的对比:
- DTFT
X ( ω ) = ∑ n = − ∞ ∞ x [ n ] e − j ω n X(\omega)=\sum_{n=-\infty}^{\infty}x[n]e^{-j\omega n} X(ω)=n=−∞∑∞x[n]e−jωn - CFT
F ( ω ) = ∫ − ∞ ∞ f ( t ) e − j ω t d t F(\omega)=\int^{\infty}_{-\infty}f(t)e^{-j\omega t}dt F(ω)=∫−∞∞f(t)e−jωtdt
对比CFT,我们可以看到DTFT和CFT的差别在于,一个自变量是 n n n,一个自变量是 t t t,一个是非连续一个是连续。所以二者对比:
- 连续信号:在CFT中,频率是连续变量,频谱 F ( ω ) F(\omega) F(ω)对应的是一个实数角频率 ω \omega ω,直接描述频率分量。
- 离散信号: 在 DTFT ( 包括DFT) 中,由于信号是离散的,频谱的周期性引入了单位圆上的频率表示。对于
X
(
ω
)
X(\omega)
X(ω)写作
X
(
e
j
ω
)
X(e^{j\omega})
X(ejω),所以DTFT写作为:
X ( e j ω ) = ∑ n = − ∞ ∞ x [ n ] e − j ω n X(e^{j\omega})=\sum_{n=-\infty}^{\infty}x[n]e^{-j\omega n} X(ejω)=n=−∞∑∞x[n]e−jωn
2.DTFT右边释义
对于DTFT右边 ∑ n = − ∞ ∞ x [ n ] e − j ω n \sum_{n=-\infty}^{\infty}x[n]e^{-j\omega n} n=−∞∑∞x[n]e−jωn我们来一步步分析这个公式的作用。
1) 复指数 e − j ω n e^{-j\omega n} e−jωn
上一篇文章中,我们用欧拉公式将极坐标表示为复指数形式:
e
j
θ
=
cos
(
θ
)
+
j
sin
(
θ
)
e^{j\theta}=\cos(\theta)+j\sin(\theta)
ejθ=cos(θ)+jsin(θ)
由此可以得到
e
−
j
ω
n
=
>
cos
(
j
ω
n
)
−
j
s
i
n
(
ω
n
)
e^{-j\omega n}=>\cos(j\omega n)-jsin(\omega n)
e−jωn=>cos(jωn)−jsin(ωn)
- 实部: cos ( j ω n ) \cos(j\omega n) cos(jωn)是以频率 ω \omega ω的余弦震荡
- 虚部: s i n ( ω n ) sin(\omega n) sin(ωn)是以频率 ω \omega ω的正弦震荡
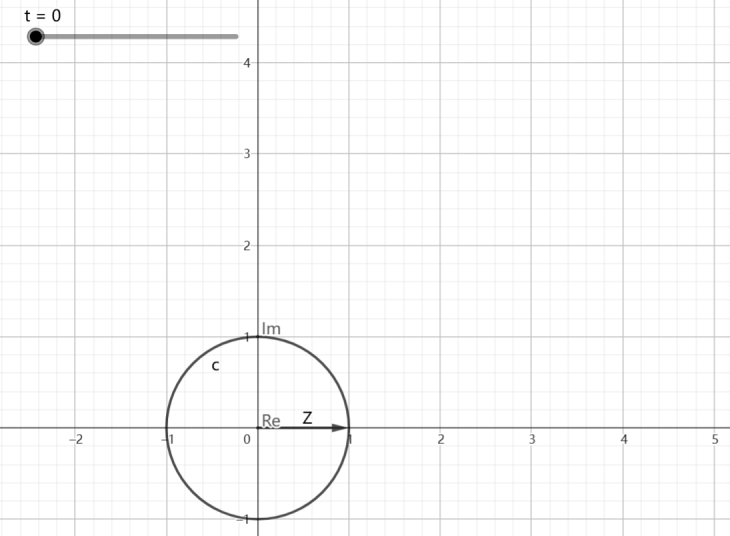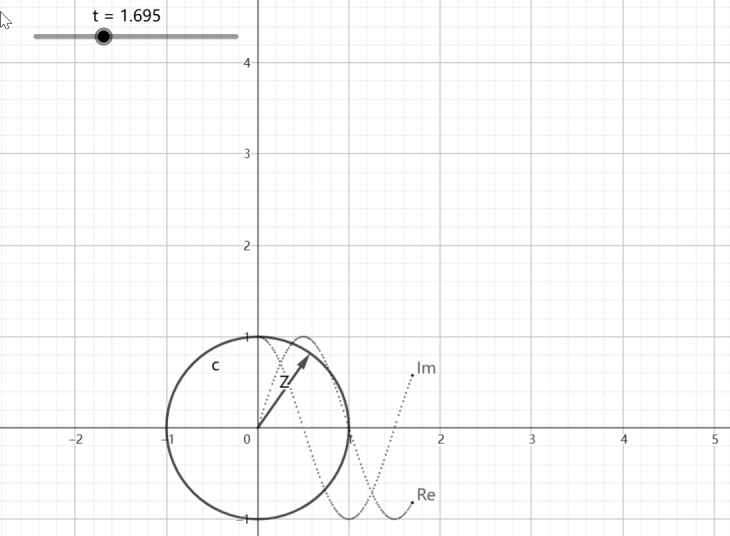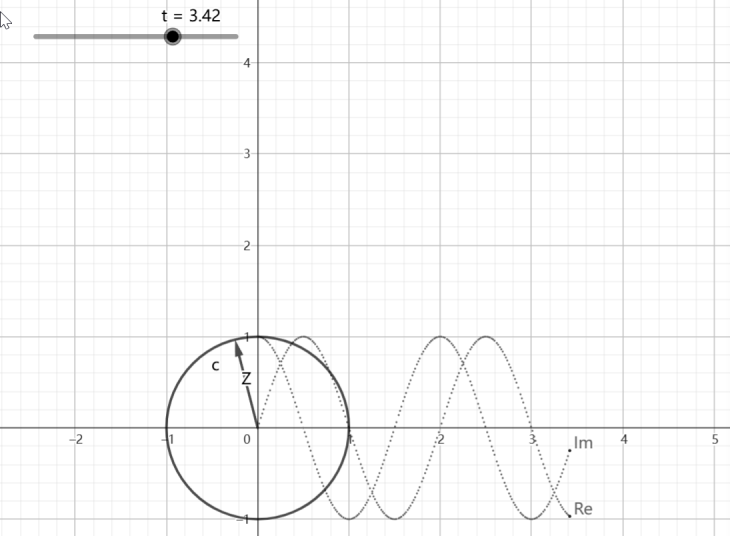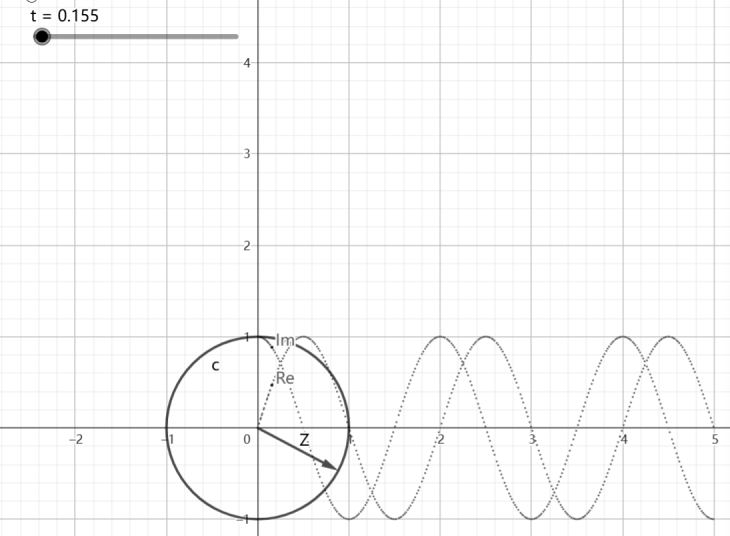
它表示的含义是随着 n n n的增长,以频率 ω \omega ω在一个单位圆上以顺时针方式进行周期震荡,如下图:
- n n n代表时间 t t t在 [ 0 , 5 ] [0,5] [0,5]区间上的变换
- Z Z Z的指向是极坐标
- I m Im Im是虚部比变化
-
R
e
Re
Re是实部变化
2)序列与复指数相乘 x [ n ] ∗ e − j ω n x[n]*e^{-j\omega n} x[n]∗e−jωn
复指数序列
在上一篇文章中,我们说 z = r ∗ e i θ z=r*e^{i\theta} z=r∗eiθ表示了极坐标的旋转, r r r代表了模长,而 x [ n ] ∗ e − j ω n x[n]*e^{-j\omega n} x[n]∗e−jωn中 x [ n ] x[n] x[n]可以是实数和虚数,所以对于 x [ n ] ∗ e − j ω n x[n]*e^{-j\omega n} x[n]∗e−jωn值得注意的是,应该理解为对于 x [ n ] x[n] x[n]进行旋转 − ω n -\omega n −ωn角度,而不是理解为模长。
而对于整个 x [ n ] x[n] x[n]的旋转,我们得到的是对于以某一个频率 ω \omega ω旋转了 − ω n -\omega n −ωn角度的新的序列,这就叫做复指数序列。其中对于 e − j ω n e^{-j\omega n} e−jωn我们看作是对于复指数序列的基函数。
复数的共轭
对于一个复数 z = a + b i z=a+bi z=a+bi,它的共轭复数为 z ‾ = a − b i \overline{z}=a-bi z=a−bi
- 复数共轭的几何意义是以实轴为对称轴反射。
- 共轭复数在许多计算中很重要,例如求复数的模:
∣
z
∣
=
z
∗
z
‾
|z|=\sqrt{z*\overline{z}}
∣z∣=z∗z,展开来为:
( a + b i ) ∗ a ( − b i ) = a 2 − a b i + a b i − b 2 ∗ i 2 , ( i 2 = − 1 ) = > a 2 + b 2 (a+bi)*a(-bi)=a^2-abi+abi-b^2*i^2,\quad (i^2=-1)=>a^2+b^2 (a+bi)∗a(−bi)=a2−abi+abi−b2∗i2,(i2=−1)=>a2+b2
复数空间的内积使用了共轭来确保以下性质:
- 共轭对称性
< f , g > = < g , f > ‾ <f,g>=\overline{<g,f>} <f,g>=<g,f> - 非负性
< f , f > ≥ 0 <f,f> \geq 0 <f,f>≥0
正交
正交:在数学中,正交(orthogonality)通常用于描述两个向量或函数之间的一种关系,表示它们彼此垂直或互不相关。
- 向量正交:在欧几里得空间中,两个向量 u , v u,v u,v 如果它们的内积为 0,则称它们是正交的,即: u ∗ v = 0 u*v=0 u∗v=0
- 函数正交:两个函数 f ( x ) , g ( x ) f(x),g(x) f(x),g(x)在区间 [ a , b ] [a,b] [a,b]上内积为0,表示为函数正交,即: < f , g > = ∫ a b f ( x ) g ( x ) ∗ d x = 0 <f,g>=\int_a^bf(x)g(x)^*dx =0 <f,g>=∫abf(x)g(x)∗dx=0
正交意味着在平面上,角度为90°,例如
(
1
,
i
)
,
(
1
,
−
i
)
(1,i),(1,-i)
(1,i),(1,−i):
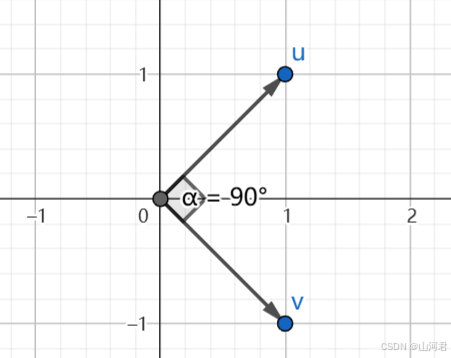
正交集
正交集是由一组两两正交的向量或函数组成的集合。在这种集合中,任意两个不同的元素的内积为 0。而对于复指数序列的基函数
e
−
j
ω
n
e^{-j\omega n}
e−jωn则有:
<
e
−
j
ω
l
n
,
e
−
j
ω
m
n
>
=
∑
n
=
0
N
−
1
e
−
j
ω
l
n
∗
(
e
−
j
ω
m
n
)
∗
(
e
−
j
ω
m
n
)
∗
=
e
j
ω
m
n
,
由于复共轭
<
e
−
j
ω
l
n
,
e
−
j
ω
m
n
>
=
∑
n
=
0
N
−
1
e
−
j
ω
l
n
∗
e
j
ω
m
n
=
>
∑
n
=
0
N
−
1
e
j
(
ω
m
−
ω
l
)
n
<e^{-j\omega_l n}, e^{-j\omega_m n}>=\sum_{n=0}^{N-1}e^{-j\omega_l n}* (e^{-j\omega_m n})^*\\ (e^{-j\omega_m n})^*=e^{j\omega_m n},\quad 由于复共轭 \\ <e^{-j\omega_l n}, e^{-j\omega_m n}>=\sum_{n=0}^{N-1}e^{-j\omega_l n}*e^{j\omega_m n} =>\\ \sum_{n=0}^{N-1}e^{j(\omega_m-\omega_l)n}
<e−jωln,e−jωmn>=n=0∑N−1e−jωln∗(e−jωmn)∗(e−jωmn)∗=ejωmn,由于复共轭<e−jωln,e−jωmn>=n=0∑N−1e−jωln∗ejωmn=>n=0∑N−1ej(ωm−ωl)n
当
ω
m
≠
ω
l
\omega_m\neq \omega_l
ωm=ωl时,
e
j
(
ω
m
−
ω
l
)
n
e^{j(\omega_m-\omega_l)n}
ej(ωm−ωl)n表示的是一个周期性复数,几何上表示在复平面上绕原点画圆,如同上文中对于
e
−
j
ω
n
e^{-j\omega n}
e−jωn解释的图像,所以对于累加和
∑
n
=
0
N
−
1
e
j
(
ω
m
−
ω
l
)
n
\sum_{n=0}^{N-1}e^{j(\omega_m-\omega_l)n}
∑n=0N−1ej(ωm−ωl)n为0。
也就是说对于任意复指数序列的基函数,当 ω m ≠ ω l \omega_m\neq \omega_l ωm=ωl时,两者之间相互不影响,这也正是DTFT使用复指数来进行运算的原因!
3)复指数序列求和
DTFT右边对于复指数序列为什么要进行求和,即 ∑ n = − ∞ ∞ x [ n ] e − j ω n \sum_{n=-\infty}^{\infty}x[n]e^{-j\omega n} ∑n=−∞∞x[n]e−jωn?
上面我们说了对于任意复指数序列的基函数,当 ω m ≠ ω l \omega_m\neq \omega_l ωm=ωl时,两者之间相互不影响。所以对于 x [ n ] ∗ e − j ω n x[n]*e^{-j\omega n} x[n]∗e−jωn中,对于某一个 ω k \omega_k ωk, x [ n ] ∗ e − j ω k n x[n]*e^{-j\omega_k n} x[n]∗e−jωkn中,将不会包含其他频率的影响。
在欧几里得空间中,投影的定义是: 投影 = < v ∗ u > u 投影=<v*u>u 投影=<v∗u>u,其中
- v v v 是要投影的向量
- u u u是基向量
- ⟨ v , u ⟩ ⟨v,u⟩ ⟨v,u⟩ 是内积,量化了 v v v 与 u u u的相似程度
而对于复指数序列投影,则有:
<
x
[
n
]
,
e
−
j
ω
n
>
=
∑
n
=
−
∞
∞
x
[
n
]
∗
e
−
j
ω
n
‾
e
−
j
ω
n
‾
=
e
j
ω
n
共轭性
<
x
[
n
]
,
e
−
j
ω
n
>
=
∑
n
=
−
∞
∞
x
[
n
]
e
−
j
ω
n
<x[n],e^{-j\omega n}>=\sum_{n=-\infty}^{\infty}x[n]*\overline{e^{-j\omega n}} \\ \overline{e^{-j\omega n}} =e^{j\omega n} 共轭性\\ <x[n],e^{-j\omega n}> =\sum_{n=-\infty}^{\infty}x[n]e^{-j\omega n}
<x[n],e−jωn>=n=−∞∑∞x[n]∗e−jωne−jωn=ejωn共轭性<x[n],e−jωn>=n=−∞∑∞x[n]e−jωn
其实就是DTFT函数,它的目的就是为了不同频率之间的影响。即如果
<
x
[
n
]
,
e
−
j
ω
k
n
>
=
∑
n
=
−
∞
∞
x
[
n
]
e
−
j
ω
k
n
=
0
<x[n],e^{-j\omega_k n}> =\sum_{n=-\infty}^{\infty}x[n]e^{-j\omega_k n}=0
<x[n],e−jωkn>=n=−∞∑∞x[n]e−jωkn=0,那么序列
x
[
n
]
x[n]
x[n]对于频率
ω
k
\omega_k
ωk没有影响。
3.DTFT左边边释义
1)实部与虚部
上文中解释了DTFT函数的由来,即
∑
n
=
−
∞
∞
x
[
n
]
e
−
j
ω
n
\sum_{n=-\infty}^{\infty}x[n]e^{-j\omega n}
∑n=−∞∞x[n]e−jωn可以看作是对信号进行“投影”,找出信号与每个频率基函数的匹配程度。那么如果
<
x
[
n
]
,
e
−
j
ω
k
n
>
=
∑
n
=
−
∞
∞
x
[
n
]
e
−
j
ω
k
n
≠
0
<x[n],e^{-j\omega_k n}> =\sum_{n=-\infty}^{\infty}x[n]e^{-j\omega_k n}\neq 0
<x[n],e−jωkn>=n=−∞∑∞x[n]e−jωkn=0这个值我们表示为
X
(
ω
k
)
X(\omega_k)
X(ωk)有什么含义?或者说有什么作用?
我们知道对于欧拉公式:
e
j
θ
=
cos
(
θ
)
+
j
sin
(
θ
)
e^{j\theta}=\cos(\theta)+j\sin(\theta)
ejθ=cos(θ)+jsin(θ)
它的实部表示了相位(两波之间的时间或空间偏移),虚部表示了幅度,那么对于DTFT公式:
X
(
e
j
ω
)
=
∑
n
=
−
∞
∞
x
[
n
]
e
−
j
ω
n
X(e^{j\omega})=\sum_{n=-\infty}^{\infty}x[n]e^{-j\omega n}
X(ejω)=n=−∞∑∞x[n]e−jωn
其中复指数通过欧拉公式得到
e
−
j
ω
n
=
cos
(
ω
n
)
−
j
sin
(
ω
n
)
e^{-j\omega n}=\cos(\omega n)-j\sin(\omega n)
e−jωn=cos(ωn)−jsin(ωn)
因此DTFT可以拆解为:
X
(
e
j
ω
)
=
∑
n
=
−
∞
∞
x
[
n
]
(
cos
(
ω
n
)
−
j
sin
(
ω
n
)
)
X
(
e
j
ω
)
=
∑
n
=
−
∞
∞
x
[
n
]
cos
(
ω
n
)
⏟
R
e
(
X
(
e
j
ω
)
)
−
∑
n
=
−
∞
∞
x
[
n
]
j
sin
(
ω
n
)
⏟
I
e
(
X
(
e
j
ω
)
)
X(e^{j\omega})=\sum_{n=-\infty}^{\infty}x[n](\cos(\omega n)-j\sin(\omega n)) \\ X(e^{j\omega})=\underbrace{\sum_{n=-\infty}^{\infty}x[n]\cos(\omega n)}_{Re(X(e^{j\omega}))}-\underbrace{\sum_{n=-\infty}^{\infty}x[n]j\sin(\omega n)}_{Ie(X(e^{j\omega}))}
X(ejω)=n=−∞∑∞x[n](cos(ωn)−jsin(ωn))X(ejω)=Re(X(ejω))
n=−∞∑∞x[n]cos(ωn)−Ie(X(ejω))
n=−∞∑∞x[n]jsin(ωn)
- R e ( X ( e j ω ) Re(X(e^{j\omega}) Re(X(ejω)是实部
- I m ( X ( e j ω ) Im(X(e^{j\omega}) Im(X(ejω)是虚部
2)幅度与相位
- 幅度:幅度是频谱中每个频率分量的强度或大小,实部和虚部的模长,可以得出该频率分量的幅度。使用
∣
X
(
e
j
ω
)
∣
|X(e^{j\omega})|
∣X(ejω)∣表示信号在频率
ω
\omega
ω处的能量强度或振幅
∣ X ( e j ω ) ∣ = R e ( X ( e j ω ) 2 + I m ( X ( e j ω ) 2 |X(e^{j\omega})|=\sqrt{Re(X(e^{j\omega})^2+Im(X(e^{j\omega})^2} ∣X(ejω)∣=Re(X(ejω)2+Im(X(ejω)2 - 相位:相位是频谱中每个频率分量相对于其他频率分量的相位偏移,通过实部和虚部的比值,可以计算相位。使用
arg
(
X
(
e
j
ω
)
)
或
∠
(
X
(
e
j
ω
)
)
\arg(X(e^{j\omega}))或\angle(X(e^{j\omega}))
arg(X(ejω))或∠(X(ejω))表示:
∠ ( X ( e j ω ) ) = tan − 1 I m ( X ( e j ω ) R e ( X ( e j ω ) \angle(X(e^{j\omega}))=\tan^{-1}\frac{Im(X(e^{j\omega})}{Re(X(e^{j\omega})} ∠(X(ejω))=tan−1Re(X(ejω)Im(X(ejω)
二、IDTFT
1.逆离散时间的傅里叶变换
上文中我们使用的傅里叶变换将序列从时域转成了频域,那么从频域恢复到时域我们成为逆傅里叶变换,逆离散时间的傅里叶变换表示为IDTFT。
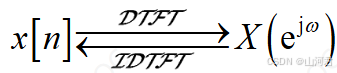
它的公式为:
x
[
n
]
=
1
2
π
∫
−
π
π
X
(
e
j
ω
)
e
j
ω
n
d
ω
x[n]=\frac{1}{2\pi}\int_{-\pi}^{\pi}X(e^{j\omega})e^{j\omega n}d\omega
x[n]=2π1∫−ππX(ejω)ejωndω
2.IDTFT验证
我们将
X
(
e
j
ω
)
X(e^{j\omega})
X(ejω)代入到公式中:
x
[
n
]
=
1
2
π
∫
−
π
π
(
∑
k
=
−
∞
∞
x
[
k
]
e
−
j
ω
k
)
e
j
ω
n
d
ω
x[n]=\frac{1}{2\pi}\int_{-\pi}^{\pi}\big(\sum_{k=-\infty}^{\infty}x[k]e^{-j\omega k}\big)e^{j\omega n}d\omega
x[n]=2π1∫−ππ(k=−∞∑∞x[k]e−jωk)ejωndω
根据之前文章积分和求和的特性
x
[
n
]
=
∑
k
=
−
∞
∞
x
[
k
]
(
1
2
π
∫
−
π
π
e
−
j
ω
(
n
−
k
)
d
w
)
x[n]=\sum_{k=-\infty}^{\infty}x[k]\big(\frac{1}{2\pi}\int_{-\pi}^{\pi}e^{-j\omega (n-k)}dw\big)
x[n]=k=−∞∑∞x[k](2π1∫−ππe−jω(n−k)dw)
先看积分项
1
2
π
∫
−
π
π
e
−
j
ω
(
n
−
k
)
d
w
\frac{1}{2\pi}\int_{-\pi}^{\pi}e^{-j\omega (n-k)}dw
2π1∫−ππe−jω(n−k)dw
- 当
k
=
n
k=n
k=n时:
1 2 π ∫ − π π e − j ω ( n − k ) d w = 1 2 π ∫ − π π 1 d w = 1 \frac{1}{2\pi}\int_{-\pi}^{\pi}e^{-j\omega (n-k)}dw=\frac{1}{2\pi}\int_{-\pi}^{\pi}1dw=1 2π1∫−ππe−jω(n−k)dw=2π1∫−ππ1dw=1 - 当
k
≠
n
k\neq n
k=n时,上文中说过,因为
e
j
(
ω
m
−
ω
l
)
n
e^{j(\omega_m-\omega_l)n}
ej(ωm−ωl)n表示的是一个周期性复数,其积分结果为零:
1 2 π ∫ − π π e − j ω ( n − k ) d w = 1 2 π ∗ 0 = 0 \frac{1}{2\pi}\int_{-\pi}^{\pi}e^{-j\omega (n-k)}dw=\frac{1}{2\pi}*0=0 2π1∫−ππe−jω(n−k)dw=2π1∗0=0
因此
1
2
π
∫
−
π
π
e
−
j
ω
(
n
−
k
)
d
w
=
{
1
,
n
=
k
0
,
n
≠
k
\frac{1}{2\pi}\int_{-\pi}^{\pi}e^{-j\omega (n-k)}dw=\begin{cases}1,\quad n=k \\ 0,\quad n\neq k\end{cases}
2π1∫−ππe−jω(n−k)dw={1,n=k0,n=k
我们用单位脉冲
δ
\delta
δ表示0,1,所以可以得到
x
[
n
]
=
∑
k
=
−
∞
∞
x
[
k
]
δ
[
n
−
k
]
x[n]=\sum_{k=-\infty}^{\infty}x[k]\delta[n-k]
x[n]=k=−∞∑∞x[k]δ[n−k]
有没有看起来很熟悉,这不就是冲激分解,使用单位冲激序列表示的加权和
总结
本篇文章中,我们对于DTFT做了深入的了解,附带着介绍了一些使用的数学知识,同时得到了IDTFT的公式。受到篇幅限制,本章只对DTFT公式进行了展示,并没有深入了解DTFT存在的条件和性质,那么在下一篇文章中会进行进一步介绍DTFT相关性质和条件。
如果对您有所帮助,请帮忙点个赞吧!