前言
reprojectImageTo3D 是 OpenCV 中用于从视差图生成三维点云的函数。它的原理是利用视差图和相机的校准参数,通过三角测量法,计算每个像素对应的三维坐标。以下内容根据源码分析所写,觉得可以的话,点赞收藏哈!!
一、基础知识
齐次坐标:齐次坐标是一种数学表示方法,它在计算机图形学和计算机视觉中被广泛使用,特别是在处理3D空间中的点和变换时。齐次坐标的主要作用有以下几点:
- 统一表示:齐次坐标允许我们使用一个统一的表示方法来处理点和向量。在笛卡尔坐标系中,点和向量是不同的概念,但通过引入齐次坐标,我们可以将它们表示为相同的形式。例如,一个3D点(x,y,z)可以表示为齐次坐标(x,y,z,1),而一个3D向量(a,b,c)可以表示为齐次坐标(a,b,c,0)。
- 简化变换:齐次坐标简化了3D空间中的线性变换,如旋转、平移和缩放。在笛卡尔坐标系中,平移不能通过矩阵乘法来表示(矩阵大小💥💥💥),但通过引入齐次坐标,平移可以表示为一个4x4矩阵与齐次坐标向量的乘法。例如,一个平移变换T=(tx,ty,tz)可以表示为以下矩阵:
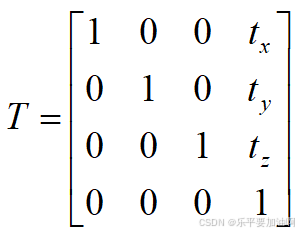
视差图:在立体视觉系统中,两个相机(称为立体相机)被放置在一定的距离(称为基线)上,同时拍摄同一场景。由于两个相机的位置不同,它们拍摄到的同一物体在两个图像中的位置会有所不同。这种位置差异就是视差(Xr-Xl💥💥💥)。视差图的大小等于图像大小,最大值为1024,最小值为0。

二、推导过程
(1)双目相机的坐标系
在双目视觉中,两个相机的几何模型如下:
- 左相机的光心位于原点 [0,0,0]其像平面位于 Z=f。
- 右相机的光心位于 [Tx,0,0],即两个相机光心的水平基线距离为 Tx。
- 像素点 (x,y) 是在左图像的像素坐标系中的位置,d=xleft−xright是视差。
(2)齐次坐标的引入
为了方便将像素坐标 (x,y)和视差 d直接映射到三维空间,引入齐次坐标系。齐次坐标将三维点扩展为四维表示:[X, Y, Z, W]。其中, [X/W,Y/W,Z/W]是三维坐标,W 是归一化因子。重点内容哈! 仅此一家哈!!💥💥💥
(3)数学公式
使用重投影矩阵 Q 与齐次坐标(x,y,d,1) 进行矩阵乘法。这一步将2D点转换为3D空间中的一个点。将得到的4维向量(X,Y,Z,W) 归一化,即除以 W 分量,得到3D空间中的点(X/W,Y/W,Z/W)。
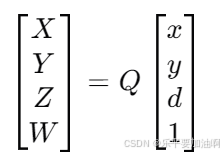
三、源码
void cv::reprojectImageTo3D( InputArray _disparity,
OutputArray __3dImage, InputArray _Qmat,
bool handleMissingValues, int dtype )
{
CV_INSTRUMENT_REGION();
Mat disparity = _disparity.getMat(), Q = _Qmat.getMat();
int stype = disparity.type();
CV_Assert( stype == CV_8UC1 || stype == CV_16SC1 ||
stype == CV_32SC1 || stype == CV_32FC1 );
CV_Assert( Q.size() == Size(4,4) );
if( dtype >= 0 )
dtype = CV_MAKETYPE(CV_MAT_DEPTH(dtype), 3);
if( __3dImage.fixedType() )
{
int dtype_ = __3dImage.type();
CV_Assert( dtype == -1 || dtype == dtype_ );
dtype = dtype_;
}
if( dtype < 0 )
dtype = CV_32FC3;
else
CV_Assert( dtype == CV_16SC3 || dtype == CV_32SC3 || dtype == CV_32FC3 );
__3dImage.create(disparity.size(), dtype);
Mat _3dImage = __3dImage.getMat();
const float bigZ = 10000.f;
Matx44d _Q;
Q.convertTo(_Q, CV_64F);
int x, cols = disparity.cols;
CV_Assert( cols >= 0 );
std::vector<float> _sbuf(cols);
std::vector<Vec3f> _dbuf(cols);
float* sbuf = &_sbuf[0];
Vec3f* dbuf = &_dbuf[0];
double minDisparity = FLT_MAX;
// NOTE: here we quietly assume that at least one pixel in the disparity map is not defined.
// and we set the corresponding Z's to some fixed big value.
if( handleMissingValues )
cv::minMaxIdx( disparity, &minDisparity, 0, 0, 0 );
for( int y = 0; y < disparity.rows; y++ )
{
float* sptr = sbuf;
Vec3f* dptr = dbuf;
if( stype == CV_8UC1 )
{
const uchar* sptr0 = disparity.ptr<uchar>(y);
for( x = 0; x < cols; x++ )
sptr[x] = (float)sptr0[x];
}
else if( stype == CV_16SC1 )
{
const short* sptr0 = disparity.ptr<short>(y);
for( x = 0; x < cols; x++ )
sptr[x] = (float)sptr0[x];
}
else if( stype == CV_32SC1 )
{
const int* sptr0 = disparity.ptr<int>(y);
for( x = 0; x < cols; x++ )
sptr[x] = (float)sptr0[x];
}
else
sptr = disparity.ptr<float>(y);
if( dtype == CV_32FC3 )
dptr = _3dImage.ptr<Vec3f>(y);
for( x = 0; x < cols; x++)
{
double d = sptr[x];
Vec4d homg_pt = _Q*Vec4d(x, y, d, 1.0);
dptr[x] = Vec3d(homg_pt.val);
dptr[x] /= homg_pt[3];
if( fabs(d-minDisparity) <= FLT_EPSILON )
dptr[x][2] = bigZ;
}
if( dtype == CV_16SC3 )
{
Vec3s* dptr0 = _3dImage.ptr<Vec3s>(y);
for( x = 0; x < cols; x++ )
{
dptr0[x] = dptr[x];
}
}
else if( dtype == CV_32SC3 )
{
Vec3i* dptr0 = _3dImage.ptr<Vec3i>(y);
for( x = 0; x < cols; x++ )
{
dptr0[x] = dptr[x];
}
}
}
}
四、总结
像素坐标到三维点:
- 像素坐标 (x,y)和视差 d 提供了物体的二维位置和深度信息。
- 重投影矩阵 Q将这些信息通过矩阵运算映射到三维空间。
视差与深度关系:
- 视差 d 越大,深度 Z 越小(物体越近。
- 齐次坐标中的 W 用于归一化三维坐标。