深入详解深度学习之神经网络基础:理解前馈神经网络与反向传播算法
深度学习作为人工智能(AI)的核心技术,已经在语音识别、图像处理、自然语言处理等诸多领域取得了显著的成果。而在深度学习的众多模型中,**前馈神经网络(Feedforward Neural Networks, FNN)与反向传播算法(Backpropagation Algorithm)**是其基础与核心。本文将深入探讨这两者的关键概念、核心原理、具体示例及其主要应用,旨在帮助读者全面理解和掌握这一重要的深度学习基础。
目录
深入详解深度学习之神经网络基础:理解前馈神经网络与反向传播算法
4. 示例:用TensorFlow实现前馈神经网络与反向传播
1. 前馈神经网络概述
定义与基本结构
前馈神经网络(FNN)是最简单且最基本的人工神经网络类型。在FNN中,信息在网络中单向流动,从输入层经过一个或多个隐藏层,最终到达输出层,没有任何形式的循环或反馈连接。这种结构类似于一条前进的流水线,信息从一端输入,经过多个处理步骤,最终输出结果。
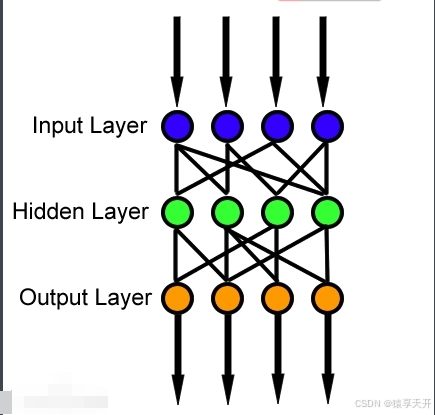
图1. 前馈神经网络示意图
神经元与激活函数
神经元(Neuron)
神经元是神经网络的基本计算单元,模拟生物神经元的功能。每个神经元接收来自前一层神经元的输入信号,通过加权和计算后,经过激活函数处理,产生输出信号传递给下一层神经元。
数学表达式:
\[
y = \phi\left(\sum_{i=1}^{n} w_i x_i + b\right)
\]
其中:
\( y \) 是神经元的输出。
\( x_i \) 是输入信号。
\( w_i \) 是对应的权重。
\( b \) 是偏置项。
\( \phi \) 是激活函数。
激活函数(Activation Function)
激活函数引入非线性,使神经网络能够拟合复杂的函数关系。常见的激活函数包括:
-
Sigmoid:
\[
\sigma(x) = \frac{1}{1 + e^{-x}}
\]
输出值在(0,1)之间,适用于二分类问题。
-
Tanh(双曲正切):
\[
\tanh(x) = \frac{e^{x} - e^{-x}}{e^{x} + e^{-x}}
\]
输出值在(-1,1)之间。
-
ReLU(Rectified Linear Unit):
\[
\text{ReLU}(x) = \max(0, x)
\]
计算简单,缓解梯度消失问题。
-
Leaky ReLU:
\[
\text{Leaky ReLU}(x) = \begin{cases}
x & \text{if } x > 0 \\
0.01x & \text{otherwise}
\end{cases}
\]
解决ReLU的“死亡”问题。
网络层次结构
一个典型的前馈神经网络由以下几层组成:
- 输入层(Input Layer):接受原始数据的特征向量,不进行任何计算。
- 隐藏层(Hidden Layers):一个或多个层,进行特征的非线性变换和抽象。
- 输出层(Output Layer):输出最终的预测结果,维度取决于具体任务(如分类类别数或回归输出维度)。
每一层由若干神经元组成,且每个神经元与前一层的所有神经元全连接(全连接层)。
2. 前馈神经网络的工作原理
前馈神经网络的运行过程主要分为**前向传播(Forward Propagation)和反向传播(Backpropagation)**两个阶段。本文首先详细介绍前向传播和损失函数的计算。
前向传播
前向传播是指将输入数据通过网络逐层传递,最终得到输出结果的过程。以下是前向传播的具体步骤:
1. 输入层:接收原始数据特征,作为网络的输入向量 \( \mathbf{x} = [x_1, x_2, \ldots, x_n] \)。
2. 隐藏层:每一隐藏层的每个神经元计算如下:
\[
z^{(l)}_j = \sum_{i=1}^{m} w^{(l)}_{ji} a^{(l-1)}_i + b^{(l)}_j
\]
\[
a^{(l)}_j = \phi(z^{(l)}_j)
\]
其中:
\( l \) 表示层数(从1开始计数)。
\( j \) 表示当前层的第 \( j \) 个神经元。
\( m \) 是前一层中的神经元数量。
\( w^{(l)}_{ji} \) 是连接前一层第 \( i \) 个神经元到当前层第 \( j \) 个神经元的权重。
\( b^{(l)}_j \) 是当前神经元的偏置。
\( \phi \) 是激活函数。
3. 输出层:与隐藏层类似,根据任务选择合适的激活函数。例如,分类任务常用Softmax函数:
\[
y^{(L)}_k = \frac{e^{z^{(L)}_k}}{\sum_{i=1}^{K} e^{z^{(L)}_i}}
\]
其中 \( L \) 是输出层,\( K \) 是类别数。
损失函数
损失函数用于衡量模型的预测结果与真实值之间的差距,是模型训练的优化目标。常见的损失函数包括:
-
均方误差(Mean Squared Error, MSE):适用于回归问题。
\[
\text{MSE} = \frac{1}{N} \sum_{i=1}^{N} (y_i - \hat{y}_i)^2
\]
-
交叉熵损失(Cross-Entropy Loss):适用于分类问题。
-
二分类交叉熵:
-
\[
\text{Loss} = -\frac{1}{N} \sum_{i=1}^{N} [y_i \log(\hat{y}_i) + (1 - y_i) \log(1 - \hat{y}_i)]
\]
-
多分类交叉熵:
\[
\text{Loss} = -\frac{1}{N} \sum_{i=1}^{N} \sum_{k=1}^{K} y_{i,k} \log(\hat{y}_{i,k})
\]
其中 \( y_{i,k} \) 是样本 \( i \) 在类别 \( k \) 上的真实标签(独热编码),\( \hat{y}_{i,k} \) 是模型的预测概率。
3. 反向传播算法详解
反向传播算法(Backpropagation Algorithm)是前馈神经网络训练中的关键算法,用于高效地计算损失函数相对于各个参数(权重和偏置)的梯度,从而通过梯度下降等优化方法更新参数,最小化损失函数。
反向传播的基本思想
反向传播的核心思想是利用链式法则(Chain Rule),从输出层开始,逐层向前计算每个参数对损失函数的贡献。这一过程包括以下几个步骤:
- 计算损失函数:通过前向传播得到预测输出,计算损失函数值。
- 计算损失函数对输出的梯度:即损失函数对网络输出的偏导数。
- 逐层计算梯度:从输出层开始,逐层向前计算每层参数对损失函数的梯度。
- 更新参数:利用计算得到的梯度,通过优化算法(如梯度下降)更新网络参数。
链式法则与梯度计算
链式法则在反向传播中的应用关键在于分解复杂的梯度计算。假设有两层网络,隐藏层与输出层,通过链式法则,可以将损失函数对隐藏层输出的梯度分解为两部分:
\[
\frac{\partial \text{Loss}}{\partial w^{(l)}_{ji}} = \frac{\partial \text{Loss}}{\partial a^{(l)}_j} \cdot \frac{\partial a^{(l)}_j}{\partial z^{(l)}_j} \cdot \frac{\partial z^{(l)}_j}{\partial w^{(l)}_{ji}}
\]
具体地,对于每一层 \( l \) 的每个神经元 \( j \),其梯度计算过程如下:
1. 输出层:
对于输出神经元 \( k \):
\[
\delta^{(L)}_k = \frac{\partial \text{Loss}}{\partial z^{(L)}_k} = \hat{y}_k - y_k
\]
(假设使用交叉熵损失与Softmax激活)
2. 隐藏层:
对于隐藏层 \( l \) 的神经元 \( j \):
\[
\delta^{(l)}_j = \left( \sum_{k=1}^{K} \delta^{(l+1)}_k w^{(l+1)}_{kj} \right) \cdot \phi'(z^{(l)}_j)
\]
其中, \( \phi' \) 是激活函数的导数。
3. 权重更新:
\[
\frac{\partial \text{Loss}}{\partial w^{(l)}_{ji}} = \delta^{(l)}_j \cdot a^{(l-1)}_i
\]
\[
w^{(l)}_{ji} = w^{(l)}_{ji} - \eta \cdot \frac{\partial \text{Loss}}{\partial w^{(l)}_{ji}}
\]
其中, \( \eta \) 是学习率。
参数更新
利用计算得到的梯度,通过优化算法(如随机梯度下降(SGD)、Adam等)对网络参数进行更新。参数更新公式如下:
\[
\theta = \theta - \eta \cdot \nabla_\theta \text{Loss}
\]
其中, \( \theta \) 表示网络的所有参数(权重与偏置), \( \eta \) 是学习率, \( \nabla_\theta \text{Loss} \) 是损失函数关于参数的梯度。
优化算法的选择会影响模型的收敛速度和最终性能。常用的优化算法有:
- 随机梯度下降(SGD):每次迭代使用一个样本更新参数。
- 小批量梯度下降(Mini-Batch Gradient Descent):每次迭代使用一个小批量样本更新参数。
- 动量法(Momentum):在SGD基础上引入动量,加速收敛。
- Adam(Adaptive Moment Estimation):结合动量法和RMSProp,自动调整学习率。
4. 示例:用TensorFlow实现前馈神经网络与反向传播
为了更直观地理解前馈神经网络与反向传播算法,下面通过使用TensorFlow和Keras框架实现一个简单的前馈神经网络,用于手写数字识别任务(MNIST数据集)。
数据准备
首先,加载MNIST数据集,并进行预处理,包括标准化和独热编码。
import tensorflow as tf
from tensorflow.keras.models import Sequential
from tensorflow.keras.layers import Dense, Flatten
from tensorflow.keras.datasets import mnist
from tensorflow.keras.utils import to_categorical
# 加载MNIST数据集
(x_train, y_train), (x_test, y_test) = mnist.load_data()
# 数据预处理
x_train = x_train.astype('float32') / 255.0 # 标准化到[0,1]
x_test = x_test.astype('float32') / 255.0
y_train = to_categorical(y_train, 10) # 独热编码
y_test = to_categorical(y_test, 10)
模型构建
构建一个包含两个隐藏层的前馈神经网络,每个隐藏层分别有128个和64个神经元,激活函数使用ReLU,输出层使用Softmax激活函数。
# 构建前馈神经网络模型
model = Sequential([
Flatten(input_shape=(28, 28)), # 输入层,将28x28的图像展平为784维向量
Dense(128, activation='relu'), # 第一个隐藏层,128个神经元,ReLU激活
Dense(64, activation='relu'), # 第二个隐藏层,64个神经元,ReLU激活
Dense(10, activation='softmax') # 输出层,10个神经元,对应10个类别,Softmax激活
])
模型编译与训练
选择Adam优化器和交叉熵损失函数,进行模型编译和训练。
# 编译模型
model.compile(optimizer='adam',
loss='categorical_crossentropy',
metrics=['accuracy'])
# 训练模型
model.fit(x_train, y_train, epochs=20, batch_size=32, validation_split=0.2)模型评估
在测试集上评估模型性能,输出测试准确率。
# 评估模型
test_loss, test_acc = model.evaluate(x_test, y_test)
print(f'测试准确率: {test_acc:.4f}')完整代码汇总:
import tensorflow as tf
from tensorflow.keras.models import Sequential
from tensorflow.keras.layers import Dense, Flatten
from tensorflow.keras.datasets import mnist
from tensorflow.keras.utils import to_categorical
# 加载MNIST数据集
(x_train, y_train), (x_test, y_test) = mnist.load_data()
# 数据预处理
x_train = x_train.astype('float32') / 255.0 # 标准化到[0,1]
x_test = x_test.astype('float32') / 255.0
y_train = to_categorical(y_train, 10) # 独热编码
y_test = to_categorical(y_test, 10)
# 构建前馈神经网络模型
model = Sequential([
Flatten(input_shape=(28, 28)), # 输入层,将28x28的图像展平为784维向量
Dense(128, activation='relu'), # 第一个隐藏层,128个神经元,ReLU激活
Dense(64, activation='relu'), # 第二个隐藏层,64个神经元,ReLU激活
Dense(10, activation='softmax') # 输出层,10个神经元,对应10个类别,Softmax激活
])
# 编译模型
model.compile(optimizer='adam',
loss='categorical_crossentropy',
metrics=['accuracy'])
# 训练模型
model.fit(x_train, y_train, epochs=20, batch_size=32, validation_split=0.2)
# 评估模型
test_loss, test_acc = model.evaluate(x_test, y_test)
print(f'测试准确率: {test_acc:.4f}')代码注释说明
数据加载与预处理:
- 使用Keras内置的MNIST数据集,包含60000个训练样本和10000个测试样本。
- 将图像像素值标准化到[0,1]区间,有助于加速训练过程。
- 将标签进行独热编码,以适应多分类的交叉熵损失函数。
模型构建:
- Flatten层:将二维28x28的图像数据展平为一维784维向量,适应全连接层的输入要求。
- Dense层:全连接层,通过设置神经元数量和激活函数,实现对数据的非线性变换。
- ReLU激活:在隐藏层中选用ReLU,提高模型的非线性表达能力。
- Softmax激活:在输出层中选用Softmax,将输出转换为概率分布,便于分类。
模型编译与训练:
- 优化器选择:Adam优化器结合了动量法和RMSProp,具有自适应学习率,适合大多数任务。
- 损失函数:交叉熵损失适用于多分类问题,能够有效衡量预测概率与真实标签之间的差异。
- 训练参数:训练20个epoch,批量大小为32,使用20%的训练数据作为验证集,监控模型的泛化性能。
模型评估:
- 在测试集上评估模型的损失和准确率,打印测试准确率以评估模型的泛化能力。
5. 前馈神经网络与反向传播的主要应用
前馈神经网络和反向传播算法在多个领域有广泛的应用,以下是其中的几个典型应用场景:
图像分类
利用前馈神经网络对图像进行分类,如手写数字识别、物体识别等。尽管卷积神经网络(CNN)在图像处理领域更为常用,但FNN仍可用于简单的图像分类任务,尤其是图像预处理后采用特征向量输入的场景。
自然语言处理(NLP)
在NLP领域,FNN可用于文本分类、情感分析等任务。将文本数据转换为固定维度的特征向量(如词袋模型、TF-IDF)后,输入FNN进行分类。
回归分析
FNN适用于回归任务,如房价预测、股票价格预测等。通过连续输出层,FNN可以对输入数据进行非线性回归,预测连续值。
医学诊断
基于患者的各项指标和症状,FNN可用于疾病预测和诊断,如糖尿病预测、癌症诊断等,帮助医生进行辅助决策。
财务预测
在金融领域,FNN可用于信用评分、风险评估等任务,通过对大量历史数据的学习,预测客户的信用风险或投资回报。
推荐系统
利用FNN对用户和物品的特征进行建模,预测用户对某个物品的喜好程度,从而实现个性化推荐,如电影推荐、商品推荐等。
6. 总结
本文深入探讨了**前馈神经网络(FNN)与反向传播算法(Backpropagation Algorithm)**的基础知识,包括关键概念、核心原理以及具体实现示例。通过理论与实践的结合,展示了FNN在各种应用场景中的潜力和优势。
关键要点总结:
-
前馈神经网络:由输入层、隐藏层和输出层组成,信息单向流动,无循环连接。适用于分类和回归等多种任务。
-
激活函数:引入非线性,常用的有ReLU、Sigmoid、Tanh等,不同任务和层选择不同的激活函数。
-
损失函数:衡量模型预测与真实值之间的差异,选择合适的损失函数对模型训练至关重要。
-
反向传播算法:利用链式法则高效计算梯度,通过优化算法更新参数,最小化损失函数。
-
优化算法:如SGD、Adam等,决定了模型参数的更新策略和收敛速度。
通过掌握这些基础知识,读者可以更好地理解深度学习模型的内部机制,进一步探索更复杂的神经网络结构和优化技术,实现更高效的AI应用。
参考资料
- 《深度学习》(Ian Goodfellow, Yoshua Bengio, Aaron Courville 著)
- Neural Networks and Deep Learning(Michael Nielsen 著)
- TensorFlow官方网站:https://www.tensorflow.org/
- Keras官方网站:https://keras.io/
- PyTorch官方网站:PyTorch
本文旨在为读者提供关于前馈神经网络与反向传播算法的全面理解,如需更深入的内容,建议参考相关专业书籍和学术论文。