聚类是无监督学习算法中的一种。聚类背后的主要思想相对简单,往往可以根据数据点之间的距离来将同类样本聚合在一起。
知识点
- K-Means
- 近邻传播
- 谱聚类
- 凝聚聚类
K-Means 聚类
K-Means 算法是所有聚类算法中最流行且最简单的算法。下面是它的工作原理:
- 选择认为最佳的类别数量 k,即样本大概可以分为多少个簇。
- 在数据空间内随机初始化 k 点为“质心”。
- 将每个观察数据点划分到于其最近的簇的质心的簇。
- 将质心更新为一个簇中所有数据点的中心。
- 重复步骤 3 和 4 步骤直到所有质心都相对稳定。
为了更好的理解 K-Means 算法的原理,这里通过一个例子来进行说明。先构建出一个数据集并画图它的分布图,该数据集含有三个簇。
import numpy as np
import matplotlib.pyplot as plt
# 构造可分为三个簇的数据
X = np.zeros((150, 2))
np.random.seed(seed=42)
X[:50, 0] = np.random.normal(loc=0.0, scale=.3, size=50)
X[:50, 1] = np.random.normal(loc=0.0, scale=.3, size=50)
X[50:100, 0] = np.random.normal(loc=2.0, scale=.5, size=50)
X[50:100, 1] = np.random.normal(loc=-1.0, scale=.2, size=50)
X[100:150, 0] = np.random.normal(loc=-1.0, scale=.2, size=50)
X[100:150, 1] = np.random.normal(loc=2.0, scale=.5, size=50)
plt.figure(figsize=(5, 5))
plt.plot(X[:, 0], X[:, 1], 'bo') 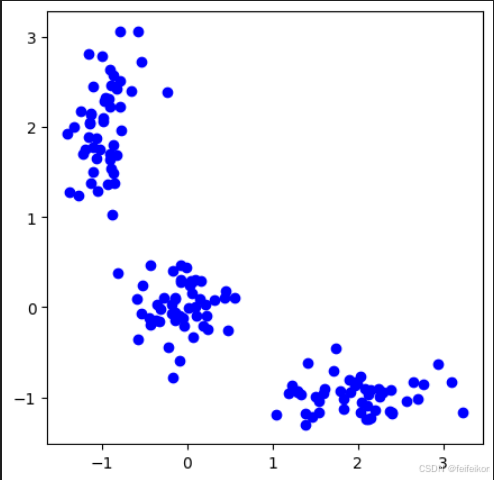
开始动手实现 K-Means 算法,K-Means 算法的实现非常简单。按照上述的算法步骤逐步实现即可。在这里,我们使用欧几里德距离来衡量两个数据点之间的距离。当然,你也可以使用其他距离度量方式。
# 调用 Scipy 库的距离计算函数,
# 用于计算数据点之间的距离
from scipy.spatial.distance import cdist
# 随机初始化三个中心点
np.random.seed(seed=42)
centroids = np.random.normal(loc=0.0, scale=1., size=6)
centroids = centroids.reshape((3, 2))
cent_history = []
cent_history.append(centroids)
for i in range(3):
# 计算每个点到中心的距离
distances = cdist(X, centroids)
# 获取数据别分到哪个簇
labels = distances.argmin(axis=1)
# 根据数据到每个簇质心的距离,标记这些点的类别
centroids = centroids.copy()
centroids[0, :] = np.mean(X[labels == 0, :], axis=0)
centroids[1, :] = np.mean(X[labels == 1, :], axis=0)
centroids[2, :] = np.mean(X[labels == 2, :], axis=0)
cent_history.append(centroids)可视化出 K-Means 算法的运行过程,以便更好地理解。
# 可视化 K 均值聚类步骤
plt.figure(figsize=(8, 8))
for i in range(4):
distances = cdist(X, cent_history[i])
labels = distances.argmin(axis=1)
plt.subplot(2, 2, i + 1)
plt.plot(X[labels == 0, 0], X[labels == 0, 1], 'bo', label='cluster #1')
plt.plot(X[labels == 1, 0], X[labels == 1, 1], 'co', label='cluster #2')
plt.plot(X[labels == 2, 0], X[labels == 2, 1], 'mo', label='cluster #3')
plt.plot(cent_history[i][:, 0], cent_history[i][:, 1], 'rX')
plt.legend(loc=0)
plt.title('Step {:}'.format(i + 1)) 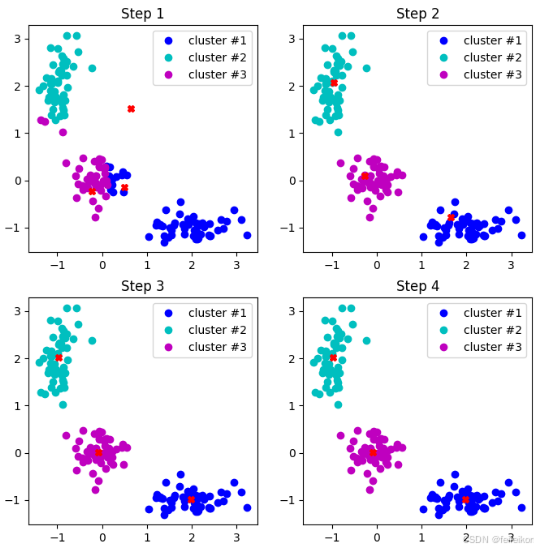
从上图中可以看出,仅用两步模型就收敛了,速度非常之快。但该算法有一个缺点,就是它对聚类质心的初始位置的很敏感,也即是随机选取的初始质心值。但是,可以多次运行算法,然后平均所有质心结果。
K-均值算法中 K 值的选择
相比于分类和回归等监督学习任务,聚类算法没有使用含标签的数据。因此,聚类需要更有效的模型评价方法。通常,当使用 K-Means 算法时,需要最小化观测数据点与其所在的簇的质心之间的平方距离之和。该值越小说明该类聚得越好。公式表达如下:
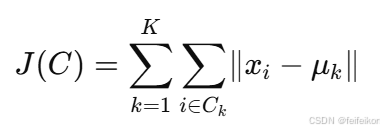

上面的定义看似合理,也就是希望数据点尽可能接近它们所属簇的质心。但也存在一个问题,当质心数(也就是 K 的值)等于样本数时,公式得到最优解,即 J(C) 达到最小。此时的每个样本都会单独把自己作为一类。这显然是没有意义的。因为这结果相当于没有进行聚类。
为了避免这种情况,我们应该定义一个函数,使得 J(C) 下降得不那么快。使用公式描述如下:
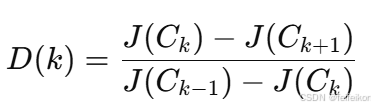
这里的含义可以理解成:
- J(Ck) 表示当我们聚成 k 簇时的目标函数值。
- 看看从 k 增加到 k+1 时,J 的降低幅度有多大,再与从 k−1 增加到 k 时的降低幅度相比。
- 如果从 k 到 k+1 的下降幅度与之前比较起来变得很小,则说明增加一个簇的收益不大,可能就不需要再继续加 K 了。
为了更好的理解,先看看一个例子。因为 scikit-learn 也提供了各种聚类算法接口,而且使用这些接口有许多优点。例如:这些算法可以并行完成,有效减少了计算时间。所以在这里为了方便,直接使用 scikit-learn 提供的 K-Means 接口进行实验。
from sklearn.cluster import KMeans # 导入 K-均值聚类模型
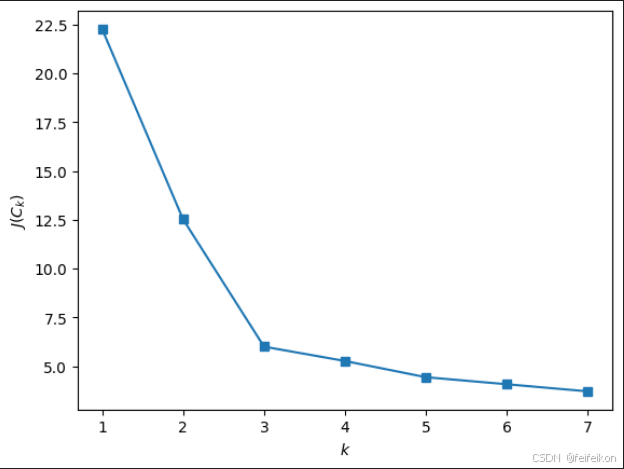
求出 K 值得选择与 J(Ck) 的关系,并画出它们的关系图。
inertia = []
for k in range(1, 8):
kmeans = KMeans(n_clusters=k, random_state=1).fit(X)
inertia.append(np.sqrt(kmeans.inertia_))
plt.plot(range(1, 8), inertia, marker='s')
plt.xlabel('$k$')
plt.ylabel('$J(C_k)$')
从上图中,可以看到当 k 小于 3 时, J(Ck)下降得非常快。之后相对平稳。这意味着选择 k 等于 3 最为合适。
K-均值存在的问题
实际上,K-Means 算法是一个 NPhard 问题。对于 n 个 d 维数据,当我们想要将其聚为 k 个簇时,K-Means 算法的复杂度为 ![]() ,这意味着模型的训练需要大量的时间。不过,这里有一些启发式方法可以缓解这个问题,例如像 MiniBatch K-Means 算法。 它每次仅采用部分数据而不是一次使用整个数据集,然后通过前面所述的方法,通过一个簇中所有观测点的平均值来移动质心。
,这意味着模型的训练需要大量的时间。不过,这里有一些启发式方法可以缓解这个问题,例如像 MiniBatch K-Means 算法。 它每次仅采用部分数据而不是一次使用整个数据集,然后通过前面所述的方法,通过一个簇中所有观测点的平均值来移动质心。
关于 K-Means 和 MiniBatch K-Means 的区别或差异可以查阅这份 scikit-learn 文档 。
近邻传播算法
近邻传播也属于聚类算法中的一种。与 K-Means 不同的是,这种方法不需要事先设置簇的数量,也就是 K 的值。近邻传播算法的主要思想是根据观测点之间的相似性来对数据进行聚类。
如果观察 xi 与观察点 xy 相似,但与观察点 xk 不相似,那么可以定义一个相似度函数 s,使得 s(xi,xj)>s(xi,xk) 。通常采用距离的负平方 ![]() 来度量两个观测点的相似性。
来度量两个观测点的相似性。

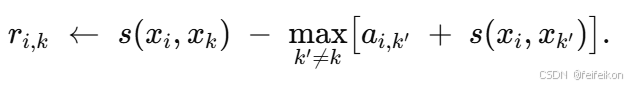




PS:故事比喻:选班长
想象一下,你在一个班级里(所有学生就是我们的样本点)。大家想要选出若干“班长”(就像要找若干聚类中心),但又不想像 K-Means 那样事先就说“我们只要 3 个班长”或“只要 5 个班长”。那该怎么办呢?班里每个人会和每个人互相传递两种信息,最终“自然而然”地选出合适的班长
-
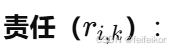
- 你可以把它理解成“学生 i 心里有多想让学生 k 当自己的班长”的程度。
- 如果学生 k 很优秀、跟 i 关系好,i 就会产生一个高的“责任值”,说:
“我觉得你就很适合当我的班长,我要死心塌地跟你混!”
- 如果发现还有另一个更牛的同学 k′,也许 iii 就会想:
“我其实更想跟那个 k′ 走呢”,
于是对 k 的“责任”就变小了。
-
可行度/可用性
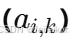 :
:- 你可以把它理解成“学生 k 愿不愿意、能不能带学生 i”的程度,也就是 k 那边对“收 i 当小弟”这事儿的支持度。
- 如果已经有很多人(或者 k 自己)都认为 k 有实力当班长,那么 k 的可行度就高:
“我(k)带这些同学还挺有把握的,我也乐意当他们的主心骨。”
- 如果 k 本身没啥意愿、或者其他人都不怎么推它当老大,它的可行度就会偏低:
“我(k)自己都不想当领头人,或者没人看好我,那就算了吧。”
谱聚类
谱聚类也是一种常用的聚类算法,其结合了上述的一些方法来创建一个性能更强的聚类方法。与其他聚类方法不同,谱聚类是一种图模型。谱聚类将观测点作为图模型的节点,将观测点之间的相似度看作为图模型中节点之间的边。在图模型中,如果两个观测点的边越短,则两个观测点就越相似。
在谱聚类中,可以通过定义观测点的相似性矩阵来存放数据样本中每两个观测点之间的相似性,通常也称为邻接矩阵。这可以采用与近邻传播算法类似的方式来构建完成:
![]()
相似矩阵相当于描绘了一张图。当图模型构建完成时,就可以对其进行切割。切割原则就是较长的边给切开。换句话说就是把相似的观测点分为一类。在形式上,这是一个 Normalized cuts 问题,如果想了解更加详细的信息,建议阅读 这篇论文。
凝聚聚类
如果你不知道要将数据样本聚为多少个簇,可以考虑使用凝聚聚类算法。凝聚聚类是所有聚类算法中相对简单,也相对容易理解的算法。
凝聚聚类的算法流程很简单,如下:
- 首先将每个观测点都作为一个簇
- 然后按降序对每两个簇中心之间距离进行排序
- 取最近的两个相邻的簇并将它们合并为一个簇,然后重新计算簇中心
- 重复步骤 2 和 3,直到所有观测点都合并到一个簇中
在每次迭代中,需要度量两个簇之间的距离。一般可以使用以下几种方法:
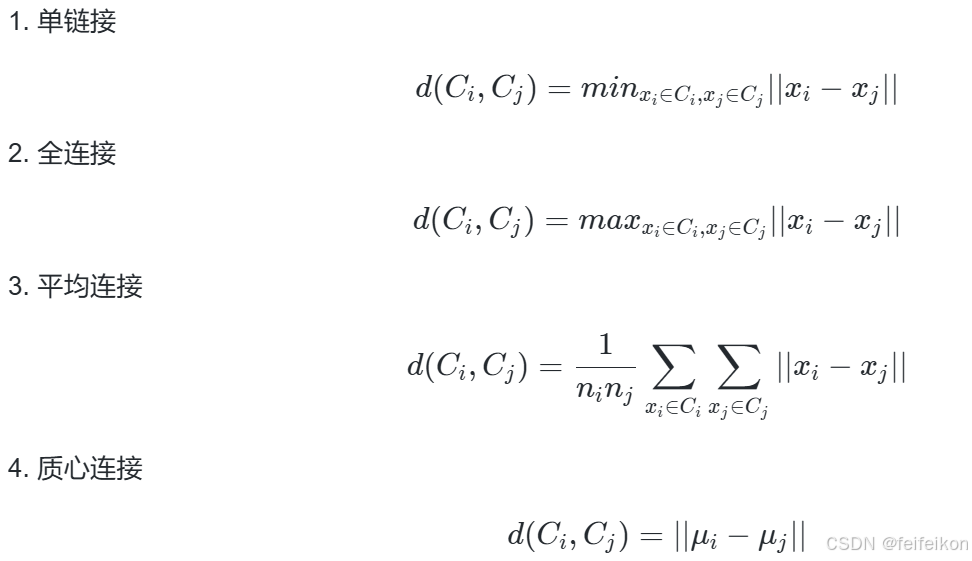
第三个平均连接是计算时间最有效的,因为它不需要在每次合并后,重新计算距离。
凝聚聚类的聚类结果可以用树状图进行表示,以帮助识别算法应该在哪一步停止以获得最佳的聚类结果。Python 也有很多工具可以构建这些树状图。
现在用凝聚聚类实现一下前面使用 K-Means 实现的聚类例子,这里直接调用 SciPy 提供的接口。
from scipy.cluster import hierarchy
from scipy.spatial.distance import pdist
X = np.zeros((150, 2))
# 构建数据集
np.random.seed(seed=42)
X[:50, 0] = np.random.normal(loc=0.0, scale=.3, size=50)
X[:50, 1] = np.random.normal(loc=0.0, scale=.3, size=50)
X[50:100, 0] = np.random.normal(loc=2.0, scale=.5, size=50)
X[50:100, 1] = np.random.normal(loc=-1.0, scale=.2, size=50)
X[100:150, 0] = np.random.normal(loc=-1.0, scale=.2, size=50)
X[100:150, 1] = np.random.normal(loc=2.0, scale=.5, size=50)
# pdist 将计算成对距离矩阵的上三角形
distance_mat = pdist(X)
# 连接 - 是一种凝聚算法的实现
Z = hierarchy.linkage(distance_mat, 'single')
plt.figure(figsize=(10, 5))
dn = hierarchy.dendrogram(Z, color_threshold=0.5)
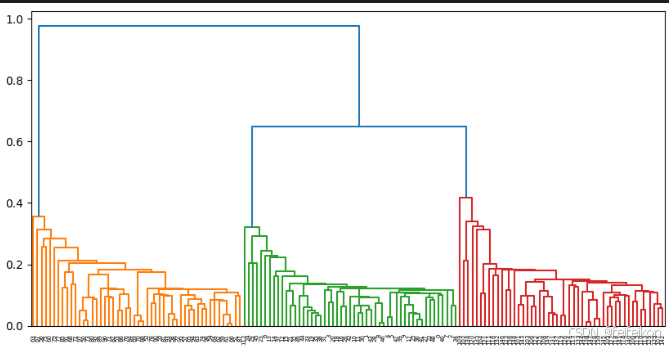
上图显示的是一个凝聚聚类的树状图。从上图可以清晰的看到整个聚类的过程:先把每个样本作为一个簇,经过多次迭代最终聚为一个簇的过程。
聚类模型评价
聚类算法与许多的监督学习算法不同,因为聚类在训练时不需要数据标签,所以不能简单地使用监督学习的评价方法来进行评价。
聚类算法通常有内部和外部的评价标准。外部评价指标是使用有关已知真实划分的信息,也就是要知道数据的真实类别。而内部指标不需要知道数据的真实类别,仅根据聚类结果来进行评估。
调整兰德指数
兰德指数是一种常用的聚类评价方法。在该评价方法中,需要知道数据的真实标签,也需要数据集的聚类结果。设 n 是样本中数据点对数的数量。设 a 表示在真实标签与聚类结果中都是同类别的观测点对数。 b 表示在真实标签与聚类结果中都是不同类别的观测点对数。兰德指数可以表示为:
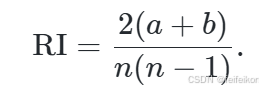
换句话说,兰德指数评估分割后的聚类结果和初始标签一致的比例。对于随机结果,RI 并不能保证分数接近 0。为了实现在聚类结果是随机产生的情况下,兰德指数应该接近零,所以有必要缩放其大小,由此得到了调整兰德指数:
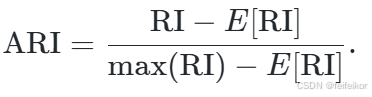
该评价方法是对称的,不依赖于标签排列顺序。因此,该指数是样本不同划分之间距离的度量。 ARI 可取 [−1,1] 范围内的值。其值越大表示聚类结果越好。
调整互信息
该评价指标与 ARI 类似。它也是对称的,不依赖于标签的具体值和排列顺序。互信息 MI 由 信息熵 函数定义,用来衡量真实数据分布与聚类结果分布的吻合程度。
同 ARI 一样,这里也定义了调整互信息 AMI 。这可以避免随着聚类数量的增加而导致 MI 指数增长。AMI 位于 [0,1] 范围内。其值越大意味着聚类结果越好。
同质性、完整性、V-mearure
从形式上来看,这些指标也是基于熵函数和条件熵函数来定义的,将聚类结果看作是离散分布:
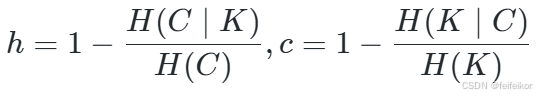

其中 K 是聚类结果,C 是原始数据。因此,h 评估的是每个簇是否由相同类别的数据点组成,c 评估的是相同类别的数据点与所属簇的匹配程度。这些指标不是对称的。两者都位于 [0,1] 范围内,而接近 1 的值表示更准确的聚类结果。这些指标的值不像 ARI 或 AMI 指标进行缩放过,因此取决于簇的数量。
当簇的数量很大且观测点的数量很小时,该评价方法也不会使评估值接近零。在这种情况下,使用 ARI 可能会更合理。但是,如果观测点超过 100 个,且簇的数量少于 10 个,此问题则可以忽略。
 轮廓系数
轮廓系数
与上述评价指标相反,轮廓系数并不需要关于原始数据的真实标签信息。仅使用聚类结果来估计聚类的质量。设 a 是数据点与一个簇内其他观测点之间距离的平均值,b 是观测点到最近簇的观测点的平均距离。则一个观测点的轮廓值为:
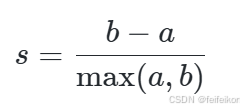
样本的轮廓值是所有样本轮廓值的平均值。该系数的取值范围为 [−1,1]。轮廓系数值越高,表示聚类的结果越好。
因此,通常如果不知道数据可以分为几类,则可以通过获取最大化轮廓系数来确定最佳聚类数 k。
一般情况下,都不需要我们去实现上述的评价方法,因为在 sklearn.metrics 接口中已经提供,只需导入即可。
最后,通过实验来看看这些指标是如何评价 MNIST 手写数字数据集的,先导入必要的模块:
from sklearn import metrics
from sklearn import datasets
import pandas as pd
from sklearn.cluster import KMeans, AgglomerativeClustering, AffinityPropagation, SpectralClustering加载数据,并构建不同的聚类算法。
data = datasets.load_digits()
X, y = data.data, data.target
algorithms = []
algorithms.append(KMeans(n_clusters=10, random_state=1))
algorithms.append(AffinityPropagation())
algorithms.append(SpectralClustering(n_clusters=10, random_state=1,
affinity='nearest_neighbors'))
algorithms.append(AgglomerativeClustering(n_clusters=10))使用不同评价指标对不同的聚类算法进行评价。
data = []
for algo in algorithms:
algo.fit(X)
data.append(({
'ARI': metrics.adjusted_rand_score(y, algo.labels_),
'AMI': metrics.adjusted_mutual_info_score(y, algo.labels_, average_method='arithmetic'),
'Homogenity': metrics.homogeneity_score(y, algo.labels_),
'Completeness': metrics.completeness_score(y, algo.labels_),
'V-measure': metrics.v_measure_score(y, algo.labels_),
'Silhouette': metrics.silhouette_score(X, algo.labels_)}))
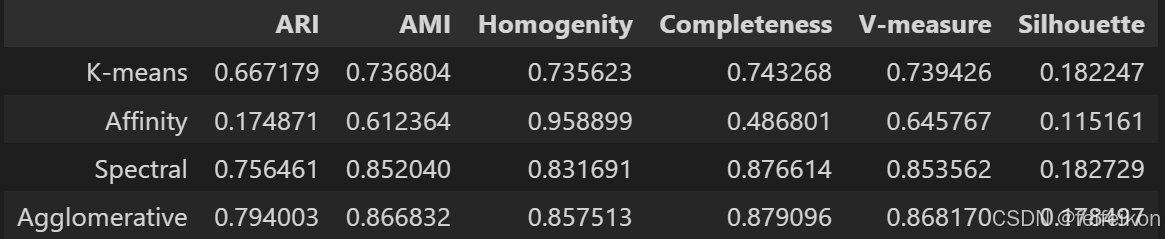
results = pd.DataFrame(data=data, columns=['ARI', 'AMI', 'Homogenity', 'Completeness',
'V-measure', 'Silhouette'],
index=['K-means', 'Affinity', 'Spectral', 'Agglomerative'])
results实验总结
本次实验主要围绕无监督学习算法进行的,主要涉及到各种聚类方法以及各种对聚类模型的评价指标。至此,相信你会对无监督学习有一个清晰的了解。