前言
遗传算法是数学建模中非常重要的一种搜索和优化算法,掌握遗传算法的精髓除了在竞赛中具有优势以外,更主要的是在解决实际问题的时候提供了一种全新的思路,通过将现实中的某种模式转换成算法,并用以解决某种问题的这种思路,或许是算法创新,提高效率的另一条路。
本文将会介绍遗传算法的思想,优缺点以及提供一个遗传算法的示例代码,此外,还会讲解父代基因的适应度高而产生的子代适应度降低的原因,以及选择的重要性。
遗传算法思想
遗传算法主要的中心思想为“适者生存,优胜劣汰”来找到全局最优解。
在遗传算法中,首先会诞生一个随机的种群,这个种群的基因库随机生成。
因为环境(目标)的限制,种群中每个个体适应环境的能力(适应度)不同,因此导致每个个体能够遗传下去的概率不同
具有更高适应度的个体会享有更高的遗传概率,即能够以自身的基因段繁殖出子代。
在繁殖过程中,两个个体的基因序列会发生交叉,从而诞生的新的个体拥有两个父代的基因段。
子代还有概率发生变异,基因序列发生突变。
在不断地迭代中,个体会发生不断地进化,适应度会提高。
需要注意的相关概念
- 初始化种群:是随机选择一组个体,每一个个体都表示一组基因序列,因此实际上是随机选择了几组基因序列
- 计算适应度:适应度是指每一个个体对环境的适应程度,也可以理解为基因的进化方向,基因在一轮一轮迭代中,尝试不断地向这个这个方向进化,以提高自身的适应度。在算法中,表现为对目标的接近程度。在实际应用中,可根据修改适应度函数,来达成自身的目的。
- 选择:选择负责繁殖下一代的个体,在实际应用中,可以调整选择的策略,比如:随机选择,提高优秀个体的选择权重,只选最优个体的等。不同的选择策略会产生不同的遗传效应。一般的选择策略都会提高更具适应性的个体被选中的概率,将遗传物质传递给下一代,但同时允许低适应性的个体也有遗传的几率,这样不会完全摒弃其遗传物质。
- 交叉:将父代的基因序列交叉,以建立新的个体(子代),交叉提高了物种进化的速度,在算法中,表现为提升迭代速度。可以有多种不同的交叉策略,主要根据实际情况做调整。
- 变异:目的是更新种群,将新模式引入基因序列中,在算法中,表现为鼓励在解空间的未知领域中探索,帮助算法跳出局部最优解。
- 物种多样性:物种的多样是意味着算法在解空间探索的广度,防止陷入某一局部最优解。增加种群的数量,采取更随机的选择策略和交叉策略,提高变异的概率等手段,皆能提高物种多样性。但过度的物种多样性可能会更容易导致子代丢失父代的优秀基因,导致迭代速度下降,甚至无法满足需求。
- 进化速度:进化速度可以理解为梯度下降时的步长,也可以理解为单次迭代时靠近最优值得速度。通过更加激进的选择策略,如:只选最优个体等,会加速进化,但同时会导致,物种多样性的降低,可能会导致陷入局部最优解。
- 参数敏感性:遗传算法对参数是具有较高的敏感度的,即,参数的修改对算法能否找到最优解,是否陷入局部最优解以及迭代速度都有较大影响。调参是门艺术,可以理解为掌握进化速度与物种多样性之间的平衡。
- 终止条件:算法的终止条件是达到迭代次数,也可以是达到了预期的值
算法优点
- 全局最优:相较于大多数的传统搜索和优化算法(尤其是基于梯度的搜索和优化算法),遗传算法更有可能找到全局最优解,而不容易陷入局部最优解(这是梯度算法的一大难点)
- 处理复杂问题:遗传算法仅需要依靠每个个体的适应度得分,而不在乎适应度函数其中的运算(即使适应度函数中包含导数等),因此它可以用于解决具有复杂数学表示的问题。
- 处理缺乏数学表示的问题:与上一条同样,遗传算法依靠的是适应度的结果而不在乎如何得出适应度的过程,因此它甚至可以用于缺乏数学表示的问题,只要在适应度函数中将逻辑表现出来,能够比较不同个体的好坏,即可运行遗传算法。
- 耐噪音:一些问题中可能存在噪音现象,这一现象会干扰到大多数的传统搜索算法,但遗传算法对此具有鲁棒性。这要归功于反复交叉和重新评估个体的操作。
- 并行处理:遗传算法非常适合并行化和分布式处理,适应度是针对每个个体独立运算,因此可以同时评估所有个体的适应度。
- 持续学习:遗传算法可以一直持续,随着环境的变化而使种群重新适应它们,但这要求环境的变化速度小于种群的进化速度。
算法缺点
- 超参数调整:遗传算法的行为由一群超参数控制,这使得研究人员需要手动调整参数,这考验研究人员的经验,在某些问题上,无法给出超参数时,遗传算法效果会大打折扣
- 计算密集:种群规模较大时可能会需要大量的计算,在达到良好结果前非常耗时,可以通过选择超参数,并行处理以及在某些情况下缓存中间值来缓解这个问题
- 过早趋同:如果某一个体的适应能力比种群的其他个体要强得多,那么它的重复性可能足以覆盖整个种群,导致算法过早的进入了局部最优值,而不会去寻找全局最优,为防止这种情况的发生,需要保证物种的多样性。
- 无法保证解的质量:遗传算法的使用并不能保证找到当前问题的全局最大值(但几乎所有的搜索和优化算法都存在此类问题,除非它是针对特定类型问题的解析解)。通常,遗传算法在适当使用时可以在合理的时间内提供良好的解决方案。
代码示例
下面给出示例代码:
import random
# 初始化种群
def initialize_population(pop_size, gene_length):
return [random.choices([0, 1], k=gene_length) for _ in range(pop_size)]
# 适应度函数的设计是为了评估一个个体的优劣性
# 通常,适应度函数是优化问题中的目标函数或其变体
def fitness_function(individual):
return sum(individual)
# 选择父代
def select_parents(population, fitnesses):
return random.choices(population, weights=fitnesses, k=2)
# 交叉方法:选择特定的交换位置,交换两个个体的基因
def crossover(parent1, parent2):
crossover_point = random.randint(1, len(parent1) - 1)
child1 = parent1[:crossover_point] + parent2[crossover_point:]
child2 = parent2[:crossover_point] + parent1[crossover_point:]
return child1, child2
# 变异方法:当随机数小于变异率时,变异:将基因值翻转
def mutate(individual, mutation_rate):
return [1 - gene if random.random() < mutation_rate else gene for gene in individual]
def genetic_algorithm(pop_size, gene_length, generations, mutation_rate):
# 初始化种群
population = initialize_population(pop_size, gene_length)
for _ in range(generations):
# 计算适应度
fitnesses = [fitness_function(ind) for ind in population]
new_population = []
for _ in range(pop_size // 2):
# 选择父代
parent1, parent2 = select_parents(population, fitnesses)
# 交叉
child1, child2 = crossover(parent1, parent2)
# 变异
new_population.extend([mutate(child1, mutation_rate), mutate(child2, mutation_rate)])
# 更新种群
population = new_population
# 选择最优个体
best_individual = max(population, key=fitness_function)
# 返回最优个体及其适应度
return best_individual, fitness_function(best_individual)
# 使用示例
best_solution, best_fitness = genetic_algorithm(pop_size=100, gene_length=20, generations=50, mutation_rate=0.01)
print(f"Best solution: {best_solution}")
print(f"Best fitness: {best_fitness}")
各函数解释
initialize_population
# 初始化种群
def initialize_population(pop_size, gene_length):
return [random.choices([0, 1], k=gene_length) for _ in range(pop_size)]
这里用了random.choices方法、列表推导式
random.choices()函数
random.choices(population, k)是 Python 的random模块中的一个函数,用于从population中随机选取k个元素,返回一个包含选定元素的列表。
population: 这是一个序列,可以是列表、元组、字符串等。random.choices()会从这个序列中随机选取元素。k: 这是一个整数,指定了要从population中选取多少个元素。
for _ in range(pop_size)这是一个列表推导式的部分。
for _ in range(pop_size)表示我们将执行pop_size次循环。
range(pop_size)生成一个从 0 到pop_size-1的序列(不包括pop_size)。_是一个常见的约定,表示这个循环变量我们并不打算使用。所以这里的_不代表任何实际的值,纯粹是用来控制循环次数。因此,
for _ in range(pop_size)表示循环pop_size次。
- 结合起来
这行代码实际上是生成一个列表,列表中包含了
pop_size个元素,每个元素都是一个长度为gene_length的列表。每个长度为gene_length的列表是通过random.choices([0, 1], k=gene_length)随机生成的,其中每个元素是从[0, 1]中选取的。
fitness_function
# 适应度函数的设计是为了评估一个个体的优劣性
# 通常,适应度函数是优化问题中的目标函数或其变体
def fitness_function(individual):
return sum(individual)
该函数为适应度函数,其目的是计算individual个体的基因序列中为1的个数。也就是说,当一个个体的基因中,1的个数越多,其适应度越高
select_parents
# 选择父代
def select_parents(population, fitnesses):
return random.choices(population, weights=fitnesses, k=2)
这里重复使用了random.choices方法,与上面的大差不差,唯一的区别是增加了weights参数
weights:
- 这是一个与
population长度相同的可迭代对象(通常是列表或元组),它表示每个元素被选中的概率权重。- 权重越大的元素被选中的概率越高。注意,权重值的大小并不是选中的概率本身,而是相对的。例如,如果
weights中的一个值是 2,而另一个是 1,那么前者的选中概率是后者的两倍。- 例如,如果
population = ['A', 'B', 'C', 'D']且weights = [0.1, 0.3, 0.5, 0.1],那么C的选中概率最大,A和D的概率最小。
crossover
# 交叉方法:选择特定的交换位置,交换两个个体的基因
def crossover(parent1, parent2):
crossover_point = random.randint(1, len(parent1) - 1)
child1 = parent1[:crossover_point] + parent2[crossover_point:]
child2 = parent2[:crossover_point] + parent1[crossover_point:]
return child1, child2
该函数随机选择了一个交叉点,crossover_point,以该点为基础作为切割,将父代分为两端,并两个相互交换一段,形成了两个新的子代。
random.randint(1,len(parent1)-1):
random.randint()会随机生成一个整数,范围从1到len(parent1)-1(parent1和parent2的长度相同)。- 选择
1到len(parent1) - 1范围内的数字是因为交叉点不能选择在序列的两端(即不允许交叉点为 0 或序列的最后一个位置)。这样可以确保父代的两部分都会参与到交叉中。
mutate
# 变异方法:当随机数小于变异率时,变异:将基因值翻转
def mutate(individual, mutation_rate):
return [1 - gene if random.random() < mutation_rate else gene for gene in individual]
这里同样采用了列表表达式,遍历一个个体内的所有基因。
如果随机数小于变异率,则会导致基因值翻转,否则基因将保持原样。
genetic_algorithm
def genetic_algorithm(pop_size, gene_length, generations, mutation_rate):
# 初始化种群
population = initialize_population(pop_size, gene_length)
for _ in range(generations):
# 计算适应度
fitnesses = [fitness_function(ind) for ind in population]
new_population = []
for _ in range(pop_size // 2):
# 选择父代
parent1, parent2 = select_parents(population, fitnesses)
# 交叉
child1, child2 = crossover(parent1, parent2)
# 变异
new_population.extend([mutate(child1, mutation_rate), mutate(child2, mutation_rate)])
# 更新种群
population = new_population
# 选择最优个体
best_individual = max(population, key=fitness_function)
# 返回最优个体及其适应度
return best_individual, fitness_function(best_individual)
- 种群初始化
generations表示世代数,即迭代次数- 计算适应度
pop_size // 2表示更新次数,因为一次更新用到两个父代,并产生两个子代,因此更新次数是种群数的1/2。//表示地板除法,结果是向下取整的商- 选择父代时,采用的是增加优秀个体的权重策略。这样保证优秀基因有更大概率遗传,也保证了其它个体有遗传的概率,不摒弃“劣质基因”
- 交叉采用的策略是定点交叉段
- 变异率为0.01,即随机数小于0.01时则会发生变异,变异策略为单个基因变异,即每个基因变异都是独立的概率,且每个基因都有概率变异
- 待更新结束后,种群更新的策略为:新产生的子代全部替代父代,形成新的种群。不保留优质父代。
从上面我们可以看到,不仅仅是适应度函数会更具不同的常见发生变化,选择函数,交叉函数,变异函数和更新种群都可以采用不同的策略。这需要使用者的智慧根据环境选择最优的策略搭配。
尤其需要注意的是,在选择策略时还要兼顾超参数的影响,避免陷入过度进化和物种多样性危机。
父代基因适应度高而子代基因适应度降低的原因
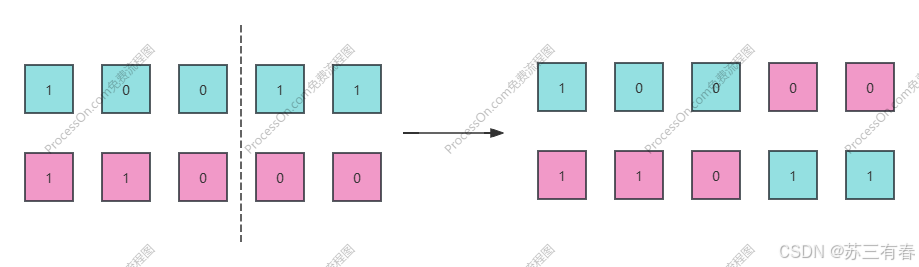
在进行交叉时,有可能出现两个父代基因的适应度高而结合后产生的子代基因的适应度反而降低的情况,
如上面的代码中,当父代1的基因序列为:[1,0,1,1,1],父代2的基因序列为:[1,1,1,0,1],此时做交叉,可能诞生的子代基因序列为:[1,0,1,0,1],基因的适应度反而降低。
1. 交叉操作引入的不利基因组合
交叉操作的基本思路是将两个父代基因的部分基因片段交换,从而产生新的子代。虽然这种方法通常能够产生适应度较高的后代,但也存在以下几种可能导致子代适应度降低的情况:
- 不良基因组合:两个适应度较高的父代可能有一些部分基因(如某些基因位的0和1组合)对适应度产生较大影响。交叉操作时,基因片段的交换可能会把这些不良基因组合带到子代中,从而降低子代的适应度。
- 局部最优:即使父代的适应度较高,但它们可能都处于某个局部最优解。如果交叉操作导致子代在搜索空间中“跳出”了父代所在的局部最优区间,可能会产生较低的适应度,甚至带来“坏”基因组合,使得子代的适应度下降。
2. 变异操作对子代的影响
变异操作在一定概率下会对个体的基因进行随机的改变。虽然变异有时能帮助算法跳出局部最优解,但也有可能导致子代的适应度下降,特别是当变异幅度过大或频率过高时。具体来说:
- 过度变异:如果变异操作过于频繁或变异幅度过大,子代可能会失去父代的优良特性,从而导致适应度下降。
- 适应度函数的复杂性:适应度函数可能会对某些特定基因组合非常敏感,稍微的变异就可能导致适应度的显著下降。
3. 遗传算法的平衡
遗传算法的设计目标是通过交叉和变异操作从父代产生更好的子代,但也不可避免地会出现"适应度降低"的情况。这种现象尤其在遗传算法的初期或未经过多代优化时较为常见。
- 探索与开发的平衡:如果在每一代中都强制选择适应度较高的个体,并进行交叉,可能会导致种群中的多样性下降,从而减缓整体的进化速度。变异和交叉可以在一定程度上提供“探索”的机制,帮助算法避免陷入局部最优解。然而,过度的探索也可能导致适应度下降。
4. 交叉操作的种类
交叉操作的具体方式也会影响其效果。不同的交叉方法(例如单点交叉、多点交叉、均匀交叉等)可能会在不同情况下对适应度产生不同的影响。某些交叉方法可能会更容易生成适应度较低的子代,而其他方法则能更好地保持或提高适应度。
5. 种群的多样性
遗传算法中的种群多样性对于防止“过早收敛”至局部最优解至关重要。如果种群的多样性减少(例如,所有个体都开始趋同于相似的基因组合),那么交叉操作可能会限制新解的生成,从而导致适应度的下降。
6. 选择压力
如果选择操作过于强烈(例如,每代仅选择适应度最高的个体进行交叉),可能会导致种群中的多样性迅速下降,甚至产生“过度优化”的现象。这样,在某些情况下,交叉出来的子代可能并不会比父代更好,反而会出现适应度下降的情况。
小结
是的,确实存在父代适应度较高时,交叉和变异操作可能导致子代适应度降低的情况。虽然遗传算法的设计目标是通过交叉和变异产生更适应环境的个体,但这种过程是随机的,并不总是能直接产生更好的解。为了应对这种问题,通常可以通过以下方法进行改进:
- 选择策略优化:适当调整选择压力,避免过早收敛。
- 交叉和变异操作调整:设计合理的交叉和变异策略,保证种群多样性,同时减少不必要的适应度降低。
- 引入精英策略:保留最优个体,确保最好的基因不会丢失。
通过这些策略,遗传算法可以在进化过程中最大程度地避免出现适应度降低的现象,同时维持算法的多样性和全局搜索能力。
选择
选择是门艺术,采取不同的选择策略会给予基因进化以不同的选择压力,不同的选择压力则会影响着基因进化的方向和速度,甚至印象基因是否进化
选择压力
选择压力是指最佳个体选中的概率与平均选中的概率的比值。
换句话说:你是否过分在意最佳个体,越提高最佳个体的选中概率,则选择压力越大,反之越小。
类比:社会中,给予有能力的人的优待越大,则压力越大(大家都拼命内卷,都想做变得比别人更出众,结果演化出有钱人表示有能力,有样貌表示有能力等,以局部能力概括全部能力的现象)。给予有能力的人的优待越小,则压力越小(大家都选择躺平,因为没有动力去成为有能力的人)。
因此,适合的压力才能更好地让推动大家进步。
在遗传算法中:
- 选择压力小(比如随机选择),会导致群体不进化
- 选择压力大(比如只选择最优个体),会导致收敛到局部最优解
选择方式
- 轮盘赌选择(随机选择):又称比例选择算子,基本思想是:个体被选中的概率与其适应度函数的比值成正比
- 确定性选择:从子代或父代中选择最优的个体
- 竞赛选择:从种群中随机选择
t个个体并记下对应适应度,返回t个个体中最好的个体,同时具备随机性和确定性
参考文章
遗传算法 (Genetic Algorithm, GA)-CSDN博客
遗传算法与深度学习实战(4)——遗传算法(Genetic Algorithm)详解与实现-CSDN博客
智能体入门——遗传算法与Qlearning_genetic algorithm和qlearning的区别和关系-CSDN博客