文章目录
0. 数据下载
算法学习、4对1辅导、论文辅导、核心期刊
项目的代码和数据下载可以通过公众号滴滴我
项目背景
这里有一个关于欧洲某商家2010年12月-2011年12月的销售数据截取的部分片段。目标是根据RF模型对顾客进行划分。
字段描述
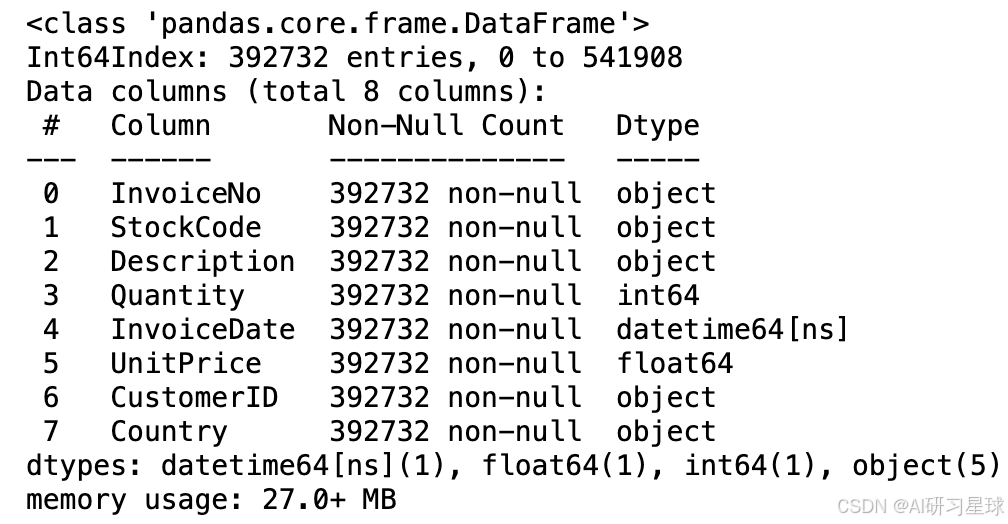
该项目有541910条数据,共8个字段,分别是InvoiceNo、StockCode、Description、Quantity、InvoiceDate、UnitPrice、CustomerID、Country。
下面是表的部分数据
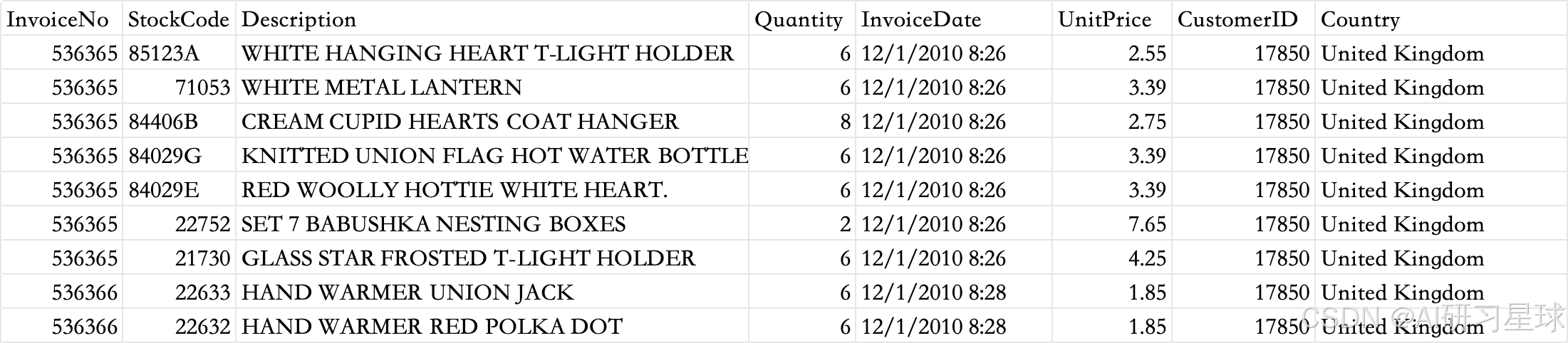
一、分析数据
1、读取数据
导入Python包
# 加载必要的库
import pandas as pd
import numpy as np
from pandas import DataFrame,Series
import seaborn as sns
import matplotlib.pyplot as plt
plt.style.use('fivethirtyeight')
%matplotlib inline
from warnings import filterwarnings
filterwarnings('ignore')
import os
import datetime
import plotly.offline as py
from plotly.offline import init_notebook_mode,iplot
import plotly.graph_objs as go
from plotly import tools
init_notebook_mode(connected=True)
import plotly.figure_factory as ff
from sklearn.cluster import MiniBatchKMeans, KMeans
from sklearn.metrics.pairwise import pairwise_distances_argmin
from sklearn.datasets import make_blobs
导入数据
# 导入数据
path='data.csv'
df=pd.read_csv(path,dtype={'CustomerID':str,'InvoiceID':str})
查看前几行数据
df.head()

查看描述统计
df.describe()
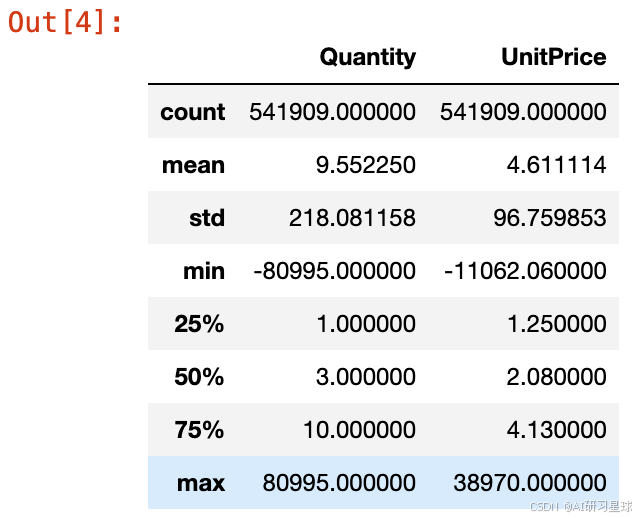
查看数据信息
df.info()
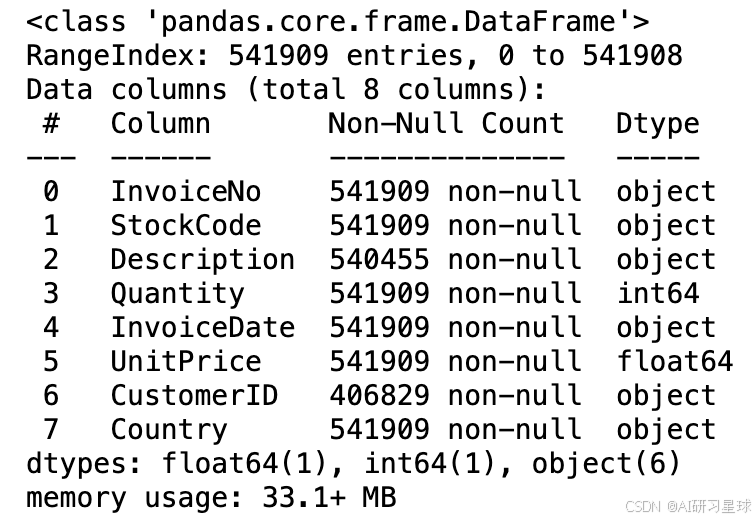
2、去除异常重复数据
df=df.drop_duplicates()
3、处理异常数据
查看描述统计
# 查看描述统计
df.describe()
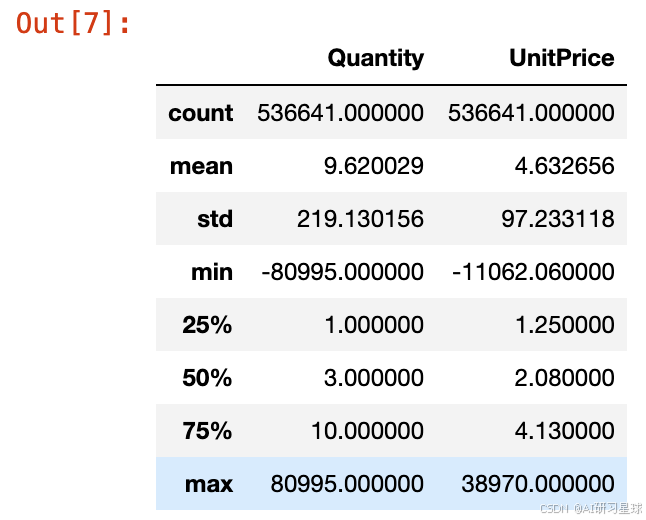
4、统计UnitPrice有多少异常的
df.loc[df['UnitPrice']<0].UnitPrice.count()
2
查看这2行的Description是什么
# 查看这2行的Description是什么
df.loc[df['UnitPrice']<0,['UnitPrice','Description']]
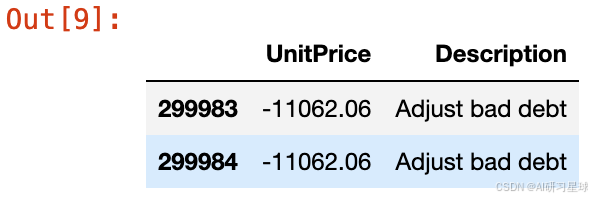
删除UnitPrice小于0的和Quantity小于0的数据
# 删除UnitPrice小于0的和Quantity小于0的数据
df=df[(df['UnitPrice']>=0) & (df['Quantity']>0)]
5、缺失值处理
# 统计缺失值
df.isnull().sum()
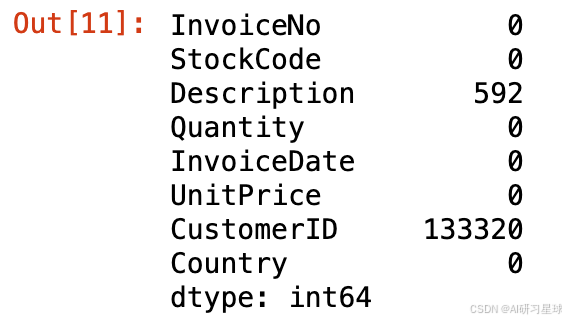
统计缺失值的占比
# 统计缺失值的占比
df.isnull().sum()/df.shape[0]*100
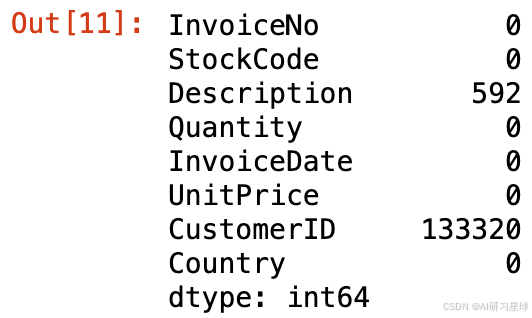
统计缺失值的占比
# 统计缺失值的占比
df.isnull().sum()/df.shape[0]*100
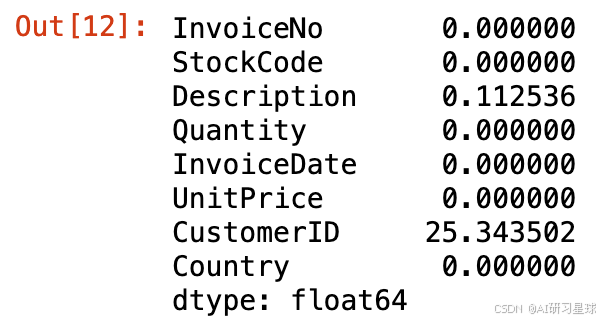
删除CustomerID为空的数据
# 删除CustomerID为空的数据
df=df[~(df.CustomerID.isnull())]
把InvoiceDate转换为datetime类型
# 把InvoiceDate转换为datetime类型
df['InvoiceDate']=pd.to_datetime(df['InvoiceDate'])
df["CustomerID"] = df["CustomerID"].astype("str")
df.info()
查看数据日期区间(需要用到最后的交易时间统计客户最后一次交易的时间距离现在的天数)
# 查看数据日期区间(需要用到最后的交易时间统计客户最后一次交易的时间距离现在的天数)
print('最大日期是:',df['InvoiceDate'].max())
print('最小日期是:',df['InvoiceDate'].min())
最大日期是: 2011-12-09 12:50:00
最小日期是: 2010-12-01 08:26:00
二、数据分析
1、数据准备
添加一列Sales
# 添加一列Sales
df['Sales']=df['Quantity']*df['UnitPrice']
# 减少重复数据
df_f = df
df_f.drop_duplicates(subset=['InvoiceNo', 'CustomerID'], keep="first", inplace=True)
#计算购买频率
frequency_df = df_f.groupby(by=['CustomerID'], as_index=False)['InvoiceNo'].count()
frequency_df.columns = ['CustomerID','Frequency']
frequency_df.set_index('CustomerID',drop=True,inplace=True)
frequency_df.head()

# 按用户ID分组计算总销售金额、最后一次交易的日期
df_group=df.groupby('CustomerID')
df_rm=df_group.agg({'Sales':'sum','InvoiceDate':'max'})
'''
通过最后一次的交易日期计算出客户最近一次下单距离2012-01-01的天数(2012-01-01,一般会用当天的
日期但由于数据是12年以前的所以这里直接用2012-01-01减去最大日期得到想要距离天数)
'''
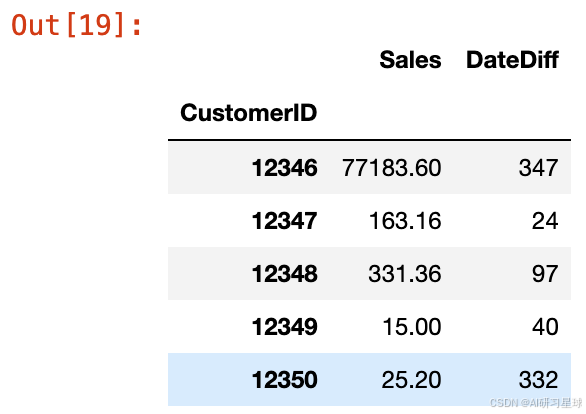
df_rm['DateDiff']=(pd.to_datetime('2012-01-01') - df_rm['InvoiceDate']).dt.days
# 删除InvoiceDate字段列
df_rm=df_rm.drop('InvoiceDate',axis=1)
df_rm.head()
# 合并数据
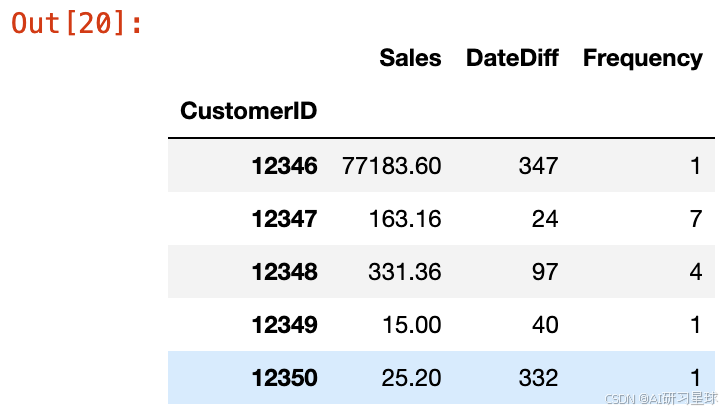
df_rfm = df_rm.merge(frequency_df,on='CustomerID')
# 对df_rfm以Sales排序
df_rfm.head()
三、数据可视化
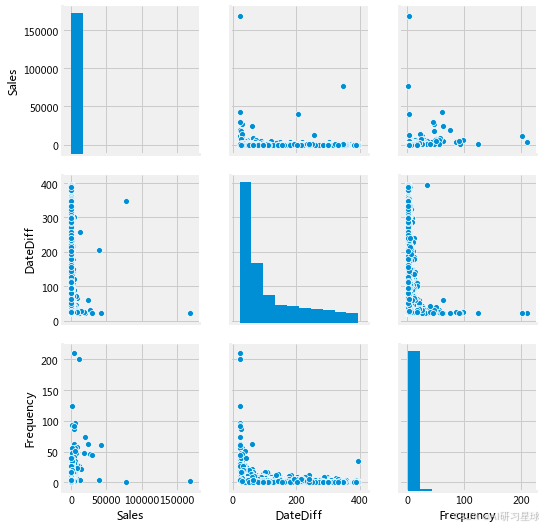
1、查看数据大概分布
sns.pairplot(df_rfm)
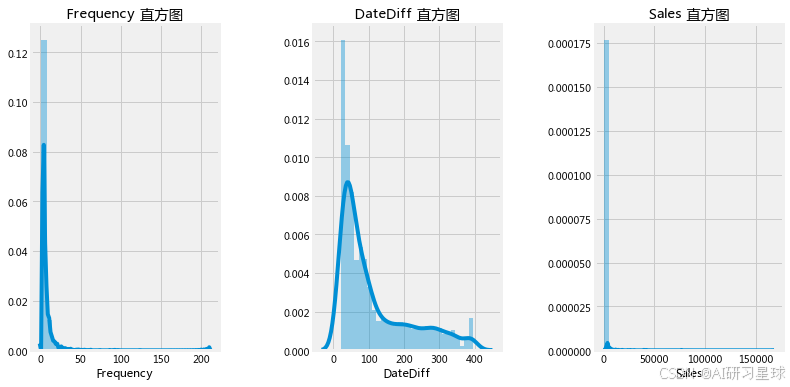
2、单独拿出来看分布直方图
plt.figure(1,figsize=(12,6))
n=0
for x in ['Frequency','DateDiff','Sales']:
n+=1
plt.subplot(1,3,n)
plt.subplots_adjust(hspace=0.5,wspace=0.5)
sns.distplot(df_rfm[x],bins=30)
plt.title('{} 直方图'.format(x))
plt.show()
3、R、F、M模型
a. R、F、M分别对应
| 对应本实例的字段 | ||
|---|---|---|
| R=Recency | 最近一次消费 | = 每个客户最近一次下单距离现在的天数 |
| F=Frequency | 消费频率 | = 每个客户累计单数 |
| M=Monetary | 消费金额 | = 每个客户累计交易金额 |
b、根据客户的消费间隔、频率和贡献金额把客户分为8个类型
k=8
clf=KMeans(n_clusters=k)
clf.fit(df_rfm)
KMeans(algorithm=‘auto’, copy_x=True, init=‘k-means++’, max_iter=300,
n_clusters=8, n_init=10, n_jobs=None, precompute_distances=‘auto’,
random_state=None, tol=0.0001, verbose=0)
c. 计算用于划分客户的阙值,R、F、M的均值(*通过分布直方图可以发现该份数据不适合用中位数来分层,因此这里用均值做分层)
rmd = df_rfm['DateDiff'].mean()
fmd = df_rfm['Frequency'].mean()
mmd = df_rfm['Sales'].mean()
rmd,fmd,mmd
(114.0414842129523, 4.271952062687255, 296.7611131597142)
def customer_type(frame):
customer_type = []
for i in range(len(frame)):
if frame.iloc[i,1]<=rmd and frame.iloc[i,2]>=fmd and frame.iloc[i,0]>=mmd:
customer_type.append('重要价值用户')
elif frame.iloc[i,1]>rmd and frame.iloc[i,2]>=fmd and frame.iloc[i,0]>=mmd:
customer_type.append('重要唤回用户')
elif frame.iloc[i,1]<=rmd and frame.iloc[i,2]<fmd and frame.iloc[i,0]>=mmd:
customer_type.append('重要深耕用户')
elif frame.iloc[i,1]>rmd and frame.iloc[i,2]<fmd and frame.iloc[i,0]>=mmd:
customer_type.append('重要挽留用户')
elif frame.iloc[i,1]<=rmd and frame.iloc[i,2]>=fmd and frame.iloc[i,0]<mmd:
customer_type.append('潜力用户')
elif frame.iloc[i,1]>rmd and frame.iloc[i,2]>=fmd and frame.iloc[i,0]<mmd:
customer_type.append('一般维持用户')
elif frame.iloc[i,1]<=rmd and frame.iloc[i,2]<fmd and frame.iloc[i,0]<mmd:
customer_type.append('新用户')
elif frame.iloc[i,1]>rmd and frame.iloc[i,2]<fmd and frame.iloc[i,0]<mmd:
customer_type.append('流失用户')
frame['classification'] = customer_type
customer_type(df_rfm)
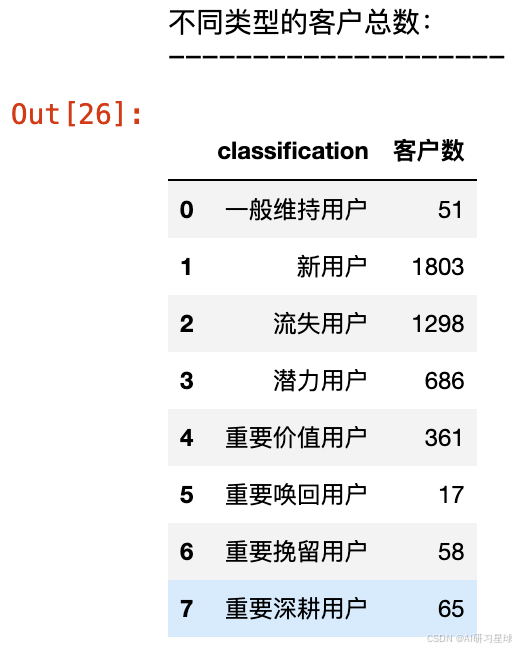
print('不同类型的客户总数:')
print('--------------------')
df_rfm.groupby(by='classification').size().reset_index(name='客户数')
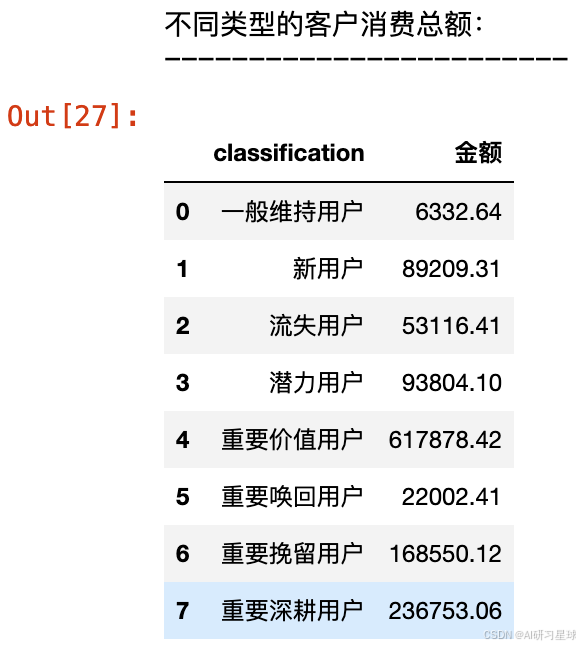
print('不同类型的客户消费总额:')
print('------------------------')
df_rfm.groupby('classification').Sales.sum().reset_index(name='金额')
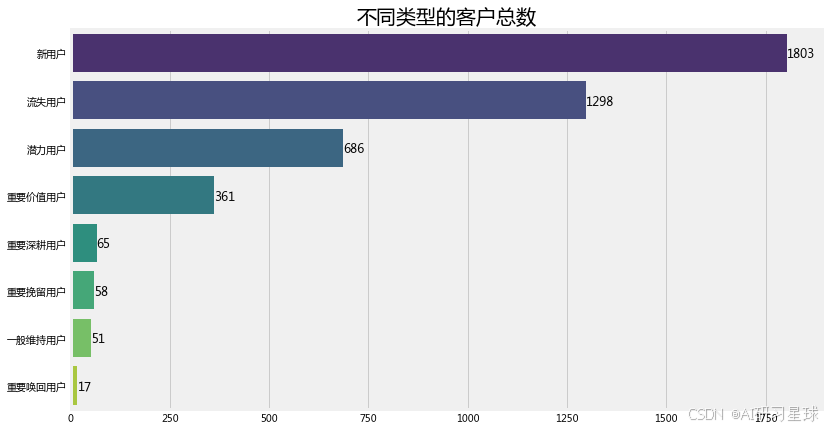
d. 可视化不同类型客户数量
plt.figure(1,figsize=(12,7))
sns.countplot(y="classification",order=df_rfm['classification'].value_counts().index ,
data=df_rfm,palette='viridis')
plt.title('不同类型的客户总数',fontsize=20)
plt.xlabel('')
plt.ylabel('')
con=list(df_rfm.groupby('classification').classification.count().values)
con=sorted(con,reverse=True)
for x,y in enumerate(con):
plt.text(y+0.1,x,'%s' %y,va='center',size=12)
plt.show()
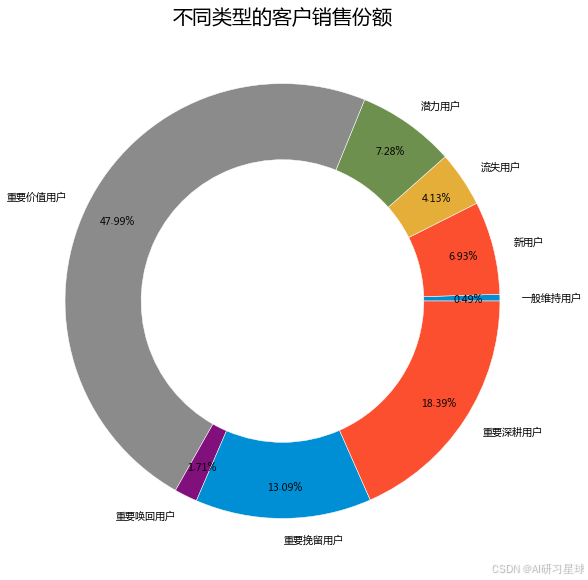
e. 不同类型的客户消费份额
plt.figure(1,figsize=(10,10))
labels=df_rfm.groupby('classification').Sales.sum().index
size=df_rfm.groupby('classification').Sales.sum()
# explode=[0,0,0,0,0.1,0,0,0]
plt.pie(size,labels=labels,autopct='%.2f%%',wedgeprops={'width':0.35,'edgecolor':'w'},
pctdistance=0.85)
plt.title('不同类型的客户销售份额',fontsize=20)
plt.axis('off')
plt.show()
4、方法二:假设不规定8个分类利用模型来选择最优分类,利用最近交易间隔,交易金额进行细分
X= df_rfm[['Sales' , 'DateDiff' ,'Frequency']].iloc[: , :].values
inertia = []
for n in range(1 , 11):
algorithm = (KMeans(n_clusters = n ,init='k-means++', n_init = 10 ,max_iter=300,
tol=0.0001, random_state= 111 , algorithm='elkan') )
algorithm.fit(X)
inertia.append(algorithm.inertia_)
algorithm = (KMeans(n_clusters = 5,init='k-means++', n_init = 10 ,max_iter=300,
tol=0.0001, random_state= 111 , algorithm='elkan') )
algorithm.fit(X)
labels3 = algorithm.labels_
centroids3 = algorithm.cluster_centers_
df_rfm['label3'] = labels3
trace1 = go.Scatter3d(
x= df_rfm['Sales'],
y= df_rfm['DateDiff'],
z= df_rfm['Frequency'],
mode='markers',
marker=dict(
color = df_rfm['label3'],
size=10,
line=dict(
color= df_rfm['label3'],
# width= 10
),
opacity=0.8
)
)
data = [trace1]
layout = go.Layout(
# margin=dict(
# l=0,
# r=0,
# b=0,
# t=0
# )
height=800,
width=800,
title= 'Sales VS DateDiff VS Frequency',
scene = dict(
xaxis = dict(title = 'Sales'),
yaxis = dict(title = 'DateDiff'),
zaxis = dict(title = 'Frequency')
)
)
fig = go.Figure(data=data, layout=layout)
py.offline.iplot(fig)
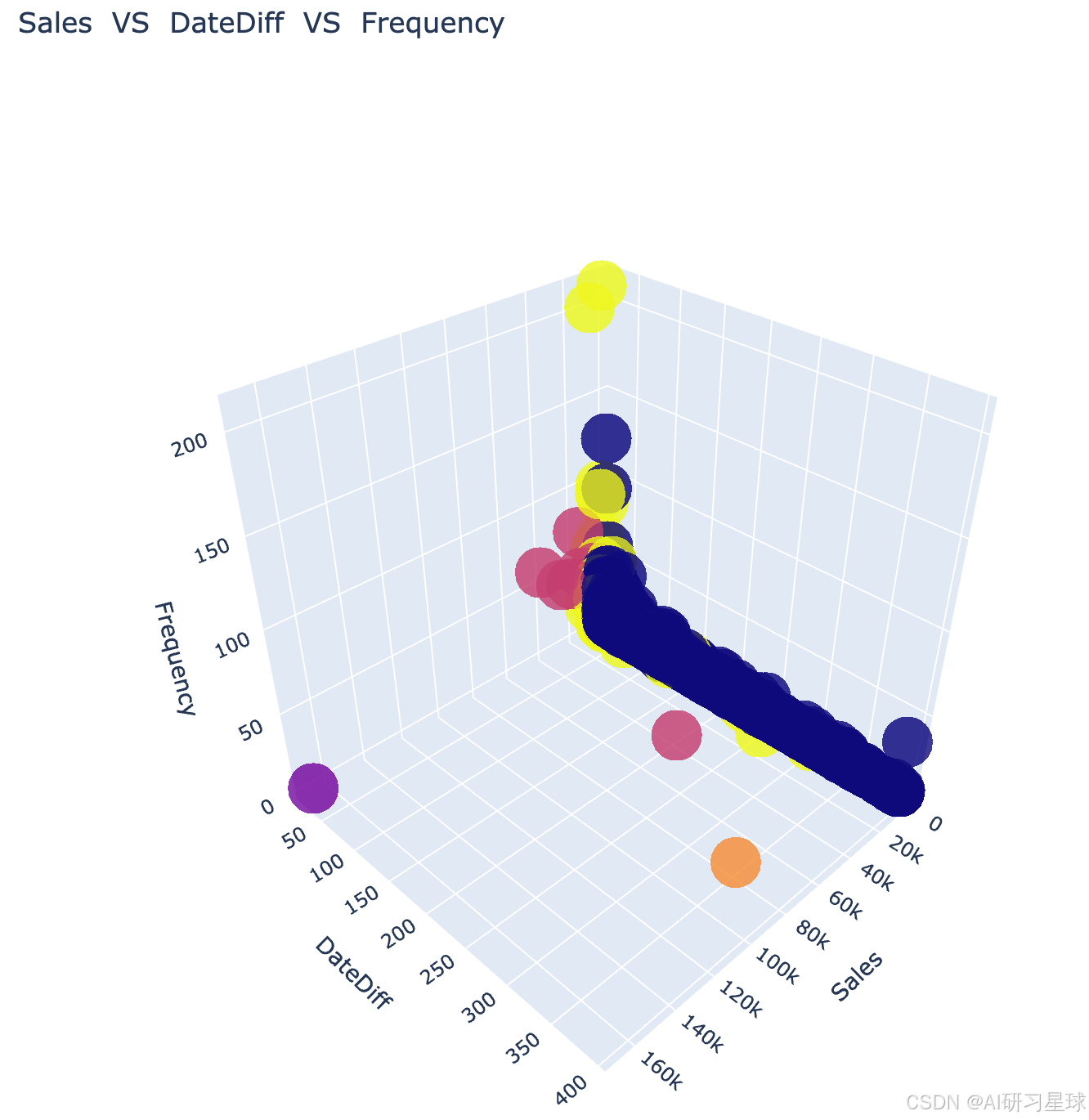
由于数据的原因,该图的视觉效果不佳,通过前面的直方分布图也可发现该份数据严重右偏态分布不适合直接利用方法二进行分类,需要先对数据进行处理和数据规范后再用方法二进行分类。