传统的离散傅里叶变换(DFT)虽然能够实现时域到频域的转换,但计算复杂度极高,对于大规模数据的处理效率十分低下。直到快速傅里叶变换(FFT)算法的出现,才极大地改变了这一局面。FFT 算法利用了信号的对称性和周期性等特性,将 DFT 的计算复杂度从原本的 大幅降低到 ,使得在实际应用中对信号进行实时、高效的频域分析成为可能。
其逆变换 IFFT 像 “时光倒流” 的魔法,可以将频域信号精准地还原回时域,保障了信号处理过程的可逆性与完整性。
FFT(快速傅里叶变换)与 IFFT(快速傅里叶逆变换)非常实用。在音频处理方面,可对含噪音频进行 FFT 变换至频域,精准定位噪声频率并去除,再用 IFFT 还原纯净音频,还能分析频谱调整频率幅值来设计独特音效;通信领域,接收端利用 FFT 将受损信号转换到频域,剖析信道引发的频率衰减并补偿,借助 IFFT 恢复原始信号保障传输无误;在图像处理上,运用二维 FFT 把图像转至频域,依据频率特性滤除干扰成分,经 IFFT 优化图像效果,同时可提取关键频率特征用于图像压缩与识别;在电力监测中,借助 FFT 分析电网电压、电流频谱,检测谐波并处理,依靠 IFFT 还原监测处理情况,确保电力系统稳定运行。
下面以MATLAB来实现方便理解:
1. 基本参数设定:
Fs = 1200; % 采样率,表示每秒采集的样本点数,这里设定为1200Hz
T = 1/Fs; % 采样周期,即相邻两个采样点的时间间隔
L = 1024; % 信号长度,意味着我们要处理的信号包含1024个采样点
t = (0:L-1)*T; % Time vector,通过这个操作生成了一个从0开始,以采样周期T为间隔,长度为L的时间向量t,它将用于后续信号在时域上的表示2. 构造原始信号与含噪信号:
接下来,我构造了原始信号 S 和含噪信号 X:
S = 0.7*sin(2*pi*100*t) + sin(2*pi*200*t);
% 这里构建了一个由两个不同频率(100Hz和200Hz)的正弦波叠加而成的原始信号
X = S + 0.2*randn(size(t));
% 在原始信号S的基础上添加了零均值的随机噪声,模拟实际应用中采集到的带有干扰的信号3.时域信号可视化
subplot(3,2,1);plot(1000*t(1:300),S(1:300));
title('S(t)初始信号');xlabel('t(s)');
ylabel('S(t)');
% 选取了原始信号S的前300个点,并将时间轴的单位转换为毫秒(乘以1000)进行绘制,展示了原始信号的局部时域波形
subplot(3,2,2);
plot( 1000*t(1:300),X(1:300))
title('X(t)受到零均值随机噪声干扰的信号');xlabel('t (ms)');ylabel('X(t)');
% 同样选取含噪信号X的前300个点,将时间轴单位转换为毫秒后绘制,方便对比观察含噪信号和原始信号在时域上的差异运行结果如图初始信号和含噪声信号 :
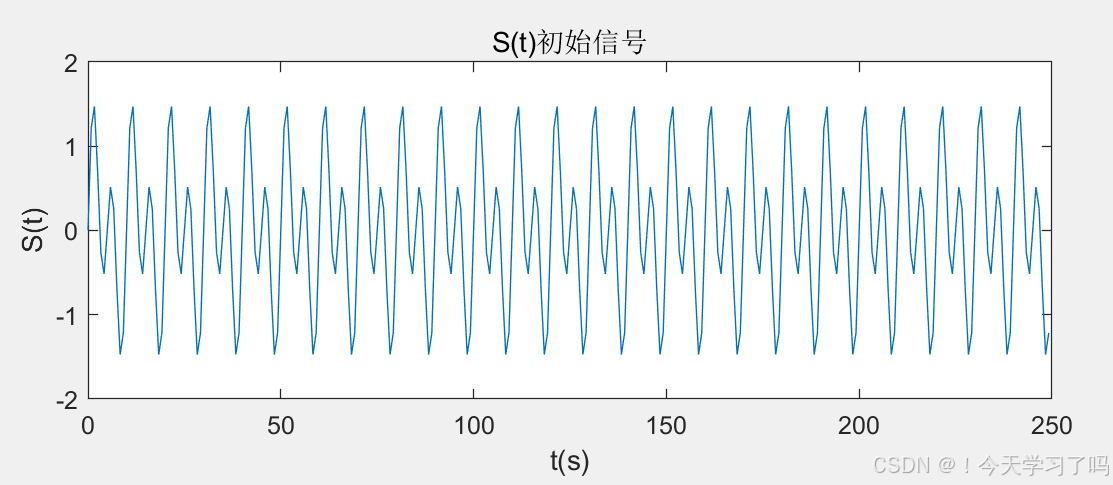
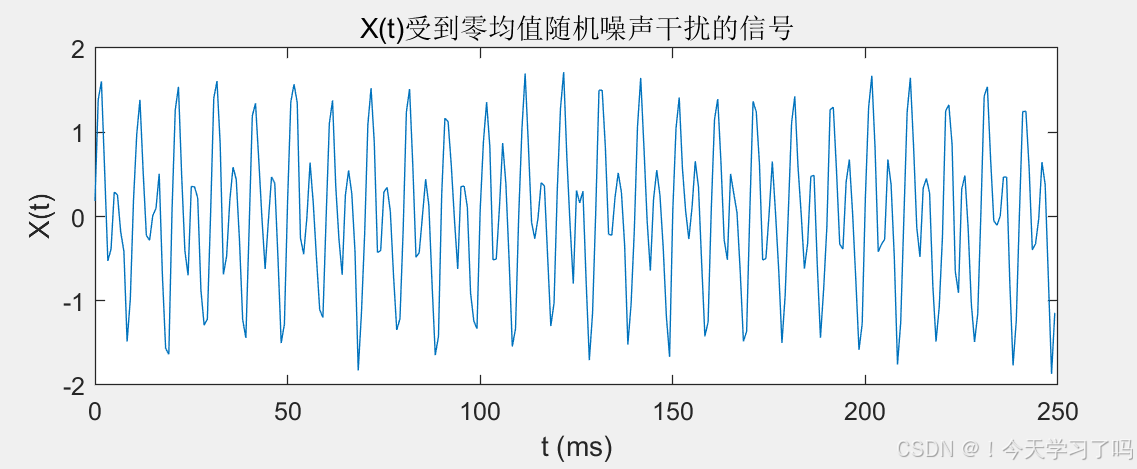
4.FFT 变换及频谱分析
Y = fft(X);
% 执行FFT操作,将时域的含噪信号X转换到频域,得到频域表示的结果Y,Y包含了信号的频率成分等信息5.幅度归一化与单面振幅谱处理
P2 = abs(Y/L); %对FFT结果进行幅度归一化处理,将幅值按照信号长度L进行归一化,使得频谱幅值更具实际物理意义
P1 = P2(1:L/2+1); % 取前L/2 + 1个点得到P1,因为FFT结果通常是双边频谱(关于频率轴原点对称),我们往往只关注单边频谱(正频率部分),所以进行这样的截取
P1(2:end-1) = 2*P1(2:end-1);
% 对除了第一个(直流分量)和最后一个点之外的中间点乘以2,这是为了得到单面振幅谱的正确幅值,因为在从双边频谱转换到单边频谱时,正频率部分的幅值需要进行这样的调整6.频率向量计算与单面振幅谱绘制
f = Fs*(0:(L/2))/L; %计算频率向量f,通过采样率Fs和信号长度L来确定频率轴的刻度,使得每个频率点对应相应的实际频率值(单位为Hz)
subplot(3,2,4);
plot(f,P1)
title('X(t)的单面振幅谱')
xlabel('f (Hz)')
ylabel('|P1(f)|')
% 绘制含噪信号X的单面振幅谱,横坐标为频率,纵坐标为对应的幅值,这样就能清晰看到信号在频域中不同频率成分的幅值分布情况原信号和含噪声信号的频谱图:
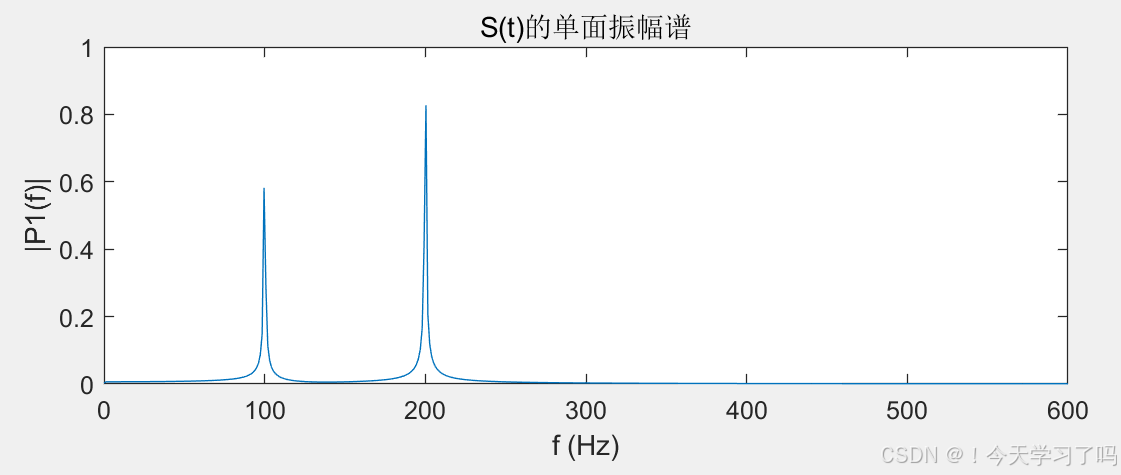
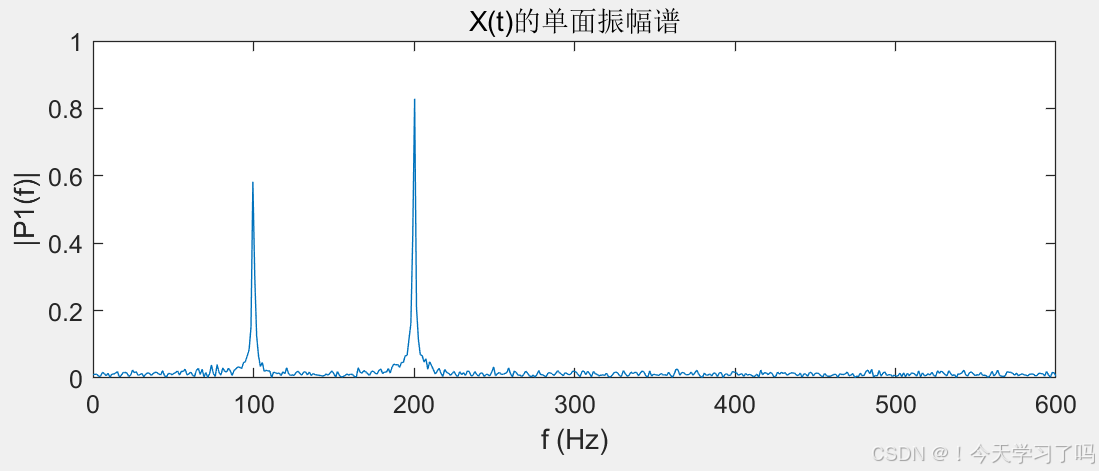
7.频域处理与小波变换(示例中的简单幅值阈值处理)
for k = 1:length(f)
if P1(k)<0.3
P1(k) = 0; % 将高于阈值的频率成分幅值设为0,这里简单模拟了一种在频域对信号进行处理的操作,比如可以类比小波变换等对信号进行滤波等操作
end
end
subplot(3, 2, 6);
plot(f,P1)
xlabel('n');
ylabel('幅值');
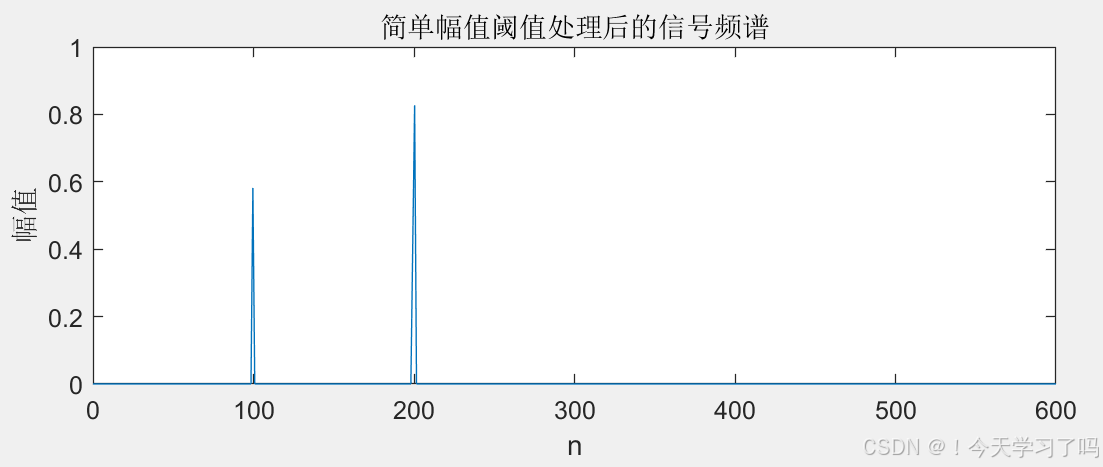
title('简单幅值阈值处理后的信号');
% 通过上述处理后再次绘制频谱图,展示经过频域处理后的信号频谱变化情况8.IFFT 逆变换恢复信号
X = ifft(Y); %逆变换恢复信号
subplot(3,2,5);
plot(t, X) % 这里添加了时间向量t作为横坐标,使时域信号能正确绘制
title('IFFT恢复后的时域信号');
xlabel('t(s)');
ylabel('X(t)');
% 绘制恢复后的时域信号波形,通过对比最初的含噪信号时域波形等,可以观察到经过一系列频域处理和逆变换后信号的变化情况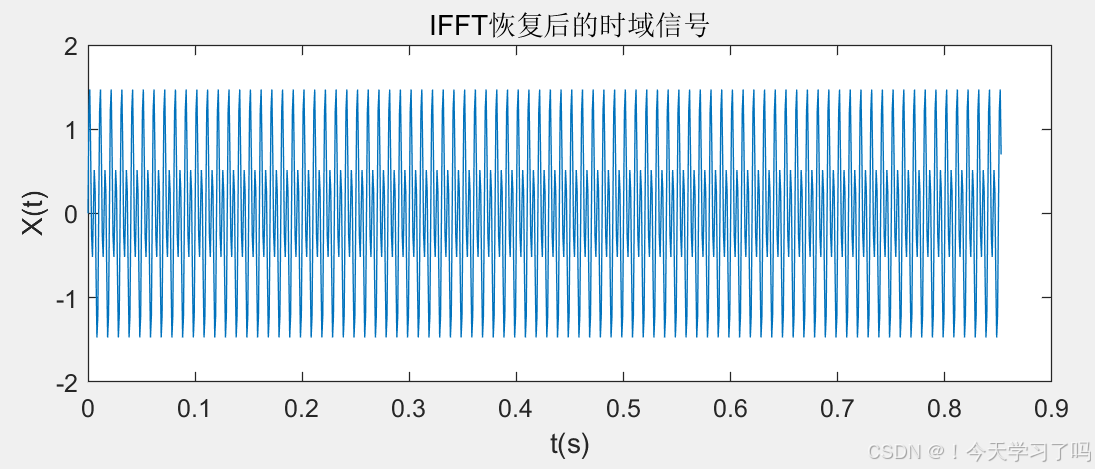
完整代码如下:
Fs = 1200; % 采样率
T = 1/Fs; % 采样周期
L = 1024; % 信号长度
t = (0:L-1)*T; % Time vector
%成了一个从 0 开始,以采样周期 T 为间隔,长度为 L 的时间向量 t
S = 0.7*sin(2*pi*100*t) + sin(2*pi*200*t);
X = S + 0.2*randn(size(t));
subplot(3,2,1);plot(1000*t(1:300),S(1:300));
title('S(t)初始信号');xlabel('t(s)');
ylabel('S(t)');
subplot(3,2,2);
plot( 1000*t(1:300),X(1:300)) %绘制含噪信号 X 的前 50 个点的时域波形
%将时间轴的单位转换为毫秒
% plot(t,X) 横轴单位为秒,绘制1500点的完整信号
% plot(1000*t,X) 横轴单位为 ms(放大了1000倍)
title('X(t)受到零均值随机噪声干扰的信号');xlabel('t (ms)');ylabel('X(t)');
Y = fft(X);
P2 = abs(Y/L); %对 FFT 结果进行幅度归一化处理
P1 = P2(1:L/2+1); % 取前 L/2 + 1 个点得到 P1
P1(2:end-1) = 2*P1(2:end-1);%对除了第一个和最后一个点之外的中间点乘以 2
%为了得到单面振幅谱的正确幅值,因为 FFT 结果是双边频谱,而这里只取了单边
f = Fs*(0:(L/2))/L; %计算频率向量 f,这里类似于 FS/N ——> 频率轴的单位值
%这三行代码可以画出双边谱
% P1 = P2(1:L);
% P1(2:end-1) = 2*P1(2:end-1);
% f = Fs*(0:(L-1))/L;
subplot(3,2,4);
plot(f,P1);
title('X(t)的单面振幅谱')
xlabel('f (Hz)')
ylabel('|P1(f)|')
Y = fft(S);
P2 = abs(Y/L);
P1 = P2(1:L/2+1);
P1(2:end-1) = 2*P1(2:end-1);
subplot(3,2,3);
plot(f,P1);
title('S(t)的单面振幅谱');
xlabel('f (Hz)');
ylabel('|P1(f)|');
for k = 1:length(f)
if P1(k)<0.3
P1(k) = 0; % 将高于阈值的频率成分幅值设为0
end
end
subplot(3, 2, 6);
plot(f,P1)
xlabel('n');
ylabel('幅值');
title('简单幅值阈值处理后的信号');
X = ifft(Y); %逆变换恢复信号
subplot(3,2,5);
plot(t, X) % 这里添加了时间向量t作为横坐标,使时域信号能正确绘制
title('IFFT恢复后的时域信号');
xlabel('t(s)');
ylabel('X(t)');