凝聚聚类
凝聚聚类(agglomerative clustering)指的是许多基于相同原则构建的聚类算法,这一原则是:算法首先声明每个点是自己的簇,然后合并两个最相似的簇,直到满足某种停止准则为止。
scikit-learn中实现的停止准则是簇的个数,因此相似的簇被合并,直到仅剩下指定个数的簇。还有一些链接(linkage)准则,规定如何度量“最相似的簇”。这种度量总是定义在两个现有的簇之间。
scikit-learn中实现了以下三种选项:
ward
默认选项。ward挑选两个簇来合并,使得所有簇中的方差增加最小。这通常会得到大小差不多相等的簇。
average
average链接将簇中所有点之间平均距离最小的两个簇合并。
complete
complete链接(也称为最大链接)将簇中点之间最大距离最小的两个簇合并。
ward 适用于大多数数据集,下面的例子中将使用它。如果簇中的成员个数非常不同(比如其中一个比其他所有都大得多),那么 average 或 complete 可能效果更好。以下示例:给出了在一个二维数据集上的凝聚聚类过程,要寻找三个簇。
import matplotlib.pyplot as plt
import mglearn
mglearn.plots.plot_agglomerative_algorithm()
plt.show()输出结果:
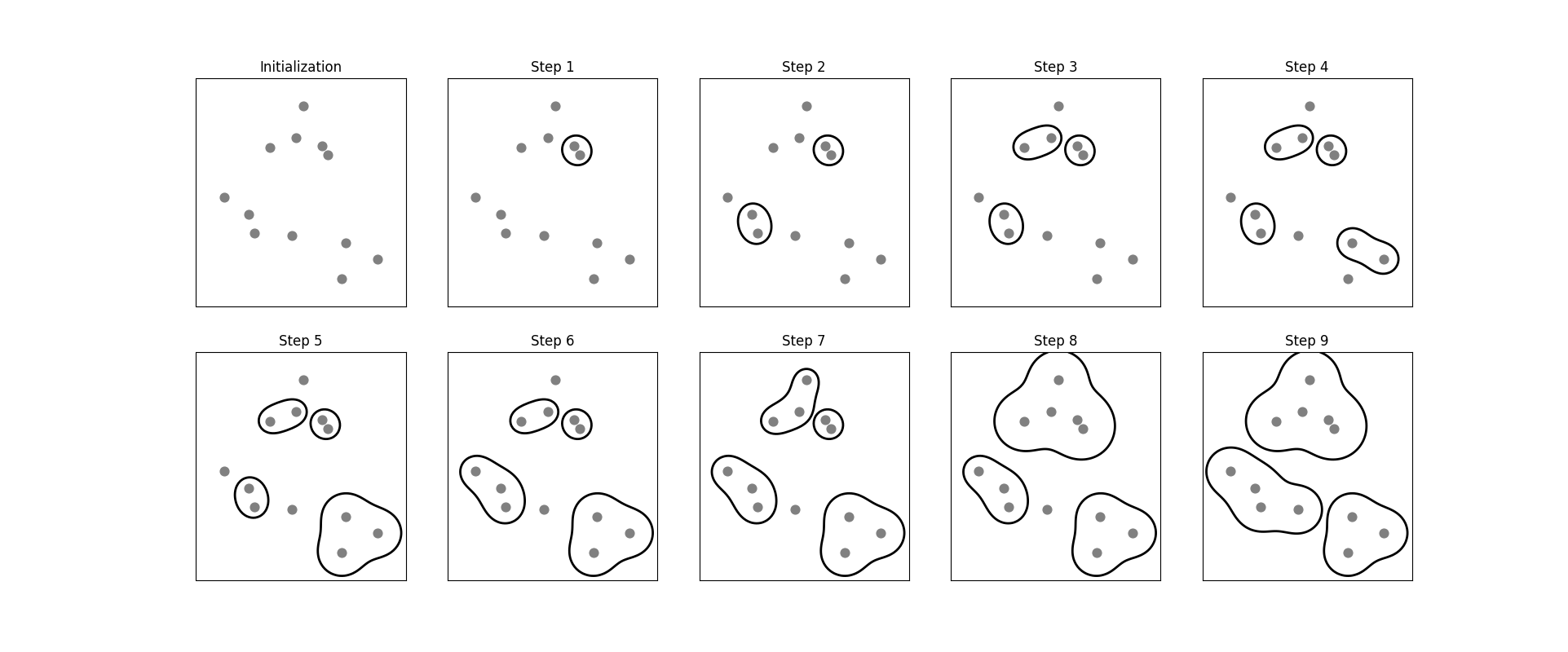
上图凝聚聚类用迭代的方式合并两个最近的簇。最开始,每个点自成一簇。然后在每一个步骤中,相距最近的两个簇被合并。在前四个步骤中,选出两个单点簇并将其合并成两点簇。在步骤5(Step 5)中,其中一个两点簇被扩展到三个点,以此类推,在步骤9(Step 9)中,只剩下3个簇。由于我们指定寻找 3 个簇,因此算法结束。
我们来看一下凝聚聚类对这里使用的简单三簇数据的效果如何。由于算法的工作原理,凝聚算法不能对新数据点做出预测。因此AgglomerativeClustering 没有predict方 法。为了构造模型并得到训练集上簇的成员关系,可以改用 fit_predict 方法。看如下示例代码:
import matplotlib.pyplot as plt
import mglearn
from sklearn.datasets import make_blobs
from sklearn.cluster import AgglomerativeClustering
X, y = make_blobs(random_state=1)
agg = AgglomerativeClustering(n_clusters=3)
assignment = agg.fit_predict(X)
mglearn.discrete_scatter(X[:, 0], X[:, 1], assignment)
plt.xlabel("Feature 0")
plt.ylabel("Feature 1")
plt.show()
输出结果:
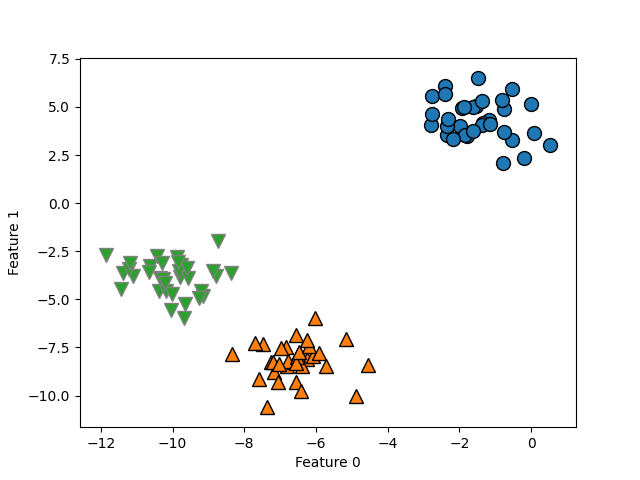
如上图,算法完美地完成了聚类。凝聚聚类的 scikit-learn 实现需要指定希望算法找到的簇的个数,但凝聚聚类方法为选择正确的个数提供了一些帮助,下面会学习。
层次聚类与树状图
凝聚聚类生成了所谓的层次聚类(hierarchical clustering)。聚类过程迭代进行,每个点都从一个单点簇变为属于最终的某个簇。每个中间步骤都提供了数据的一种聚类(簇的个数也不相同)。有时候,同时查看所有可能的聚类是有帮助的。下一个例子叠加显示了我们第一个例子中所有可能的聚类,有助于深入了解每个簇如何分解为较小的簇:
import matplotlib.pyplot as plt
import mglearn
mglearn.plots.plot_agglomerative()
plt.show()输出:
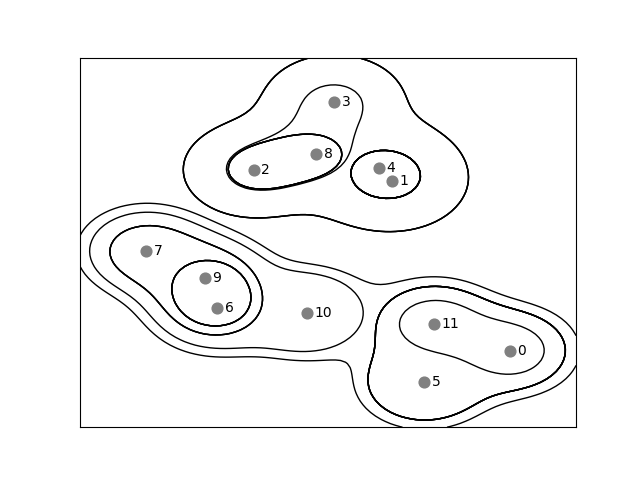
上图是凝聚聚类生成的层次化的簇分配(用线表示)以及带有编号的数据点。虽然这种可视化为层次聚类提供了非常详细的视图,但它依赖于数据的二维性质,因此不能用于具有两个以上特征的数据集。但还有另一个将层次聚类可视化的工具,叫作树状图 (dendrogram),它可以处理多维数据集。
然而目前 scikit-learn 没有绘制树状图的功能。但可以利用SciPy轻松生成树状 图。SciPy的聚类算法接口与scikit-learn的聚类算法稍有不同。SciPy提供了一个函数, 接受数据数组X并计算出一个链接数组(linkage array),它对层次聚类的相似度进行编码。 然后我们可以将这个链接数组提供给scipy的dendrogram函数来绘制树状图,如下:
import matplotlib.pyplot as plt
from sklearn.datasets import make_blobs
# 从SciPy中导入dendrogram函数和ward聚类函数
from scipy.cluster.hierarchy import dendrogram, ward
X, y = make_blobs(random_state=0, n_samples=12)
# 将ward聚类应用于数据数组X
# SciPy的ward函数返回一个数组,指定执行凝聚聚类时跨越的距离
linkage_array = ward(X)
# 现在为包含簇之间距离的linkage_array绘制树状图
dendrogram(linkage_array)
# 在树中标记划分成两个簇或三个簇的位置
ax = plt.gca()
bounds = ax.get_xbound()
ax.plot(bounds, [7.25, 7.25], '--', c='k')
ax.plot(bounds, [4, 4], '--', c='k')
ax.text(bounds[1], 7.25, ' two clusters', va='center', fontdict={'size': 15})
ax.text(bounds[1], 4, ' three clusters', va='center', fontdict={'size': 15})
plt.xlabel("Sample index")
plt.ylabel("Cluster distance")
plt.show()输出结果:
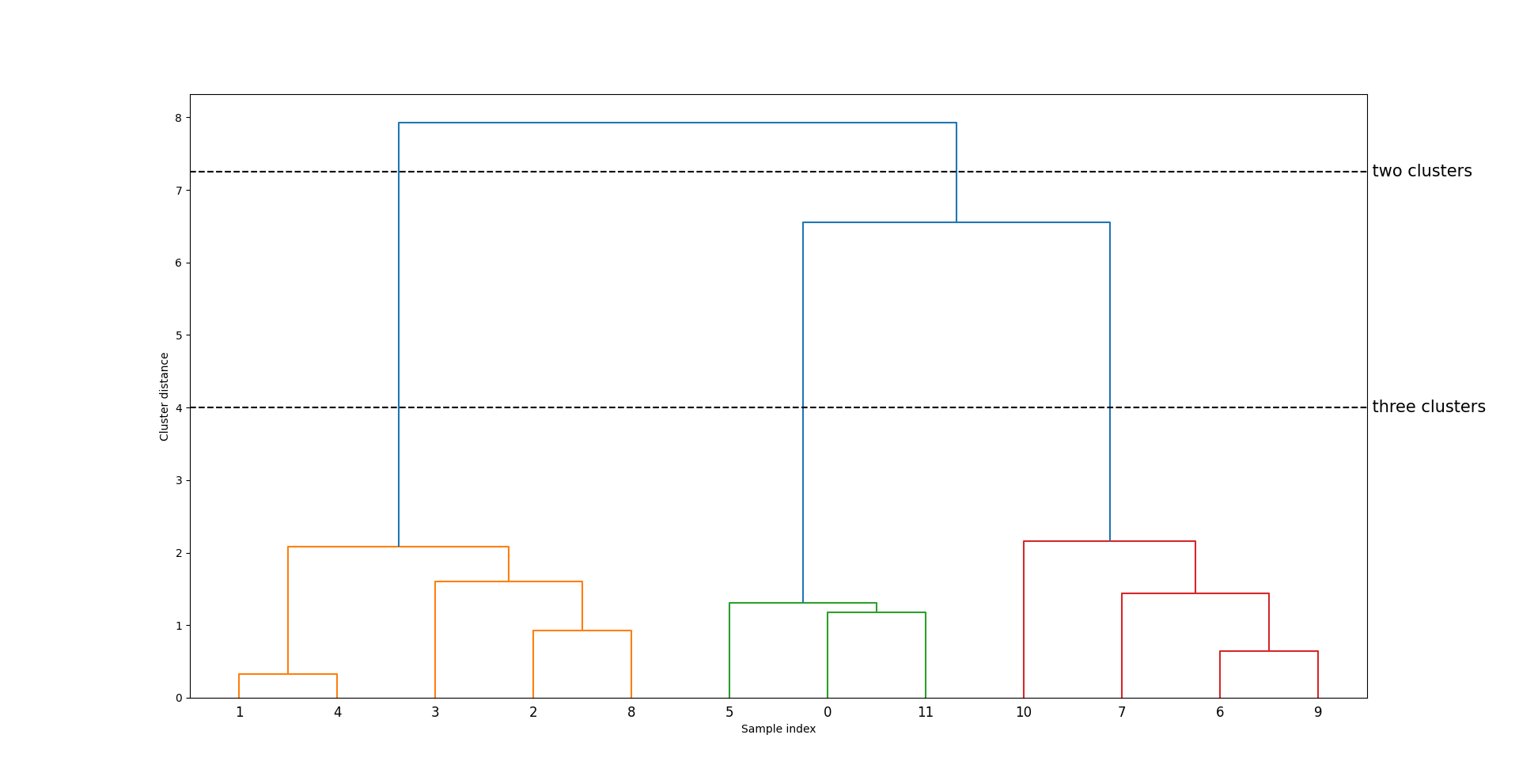
这个图是上图中聚类的树状图(用线表示划分成两个簇和三个簇)。
树状图在底部显示数据点(编号从 0 到 11)。然后以这些点(表示单点簇)作为叶节点绘制一棵树,每合并两个簇就添加一个新的父节点。 从下往上看,数据点 1 和 4 首先被合并。接下来,点 6 和 9 被合并为一个簇,以此类推。在顶层有两个分支,一个由点 11、0、5、10、7、6 和 9 组成, 另一个由点 1、4、3、2 和 8 组成。这对应于图中左侧两个最大的簇。
树状图的 y 轴不仅说明凝聚算法中两个簇何时合并,每个分支的长度还表示被合并的簇之间的距离。在这张树状图中,最长的分支是用标记为“three clusters”(三个簇)的虚线表示的三条线。它们是最长的分支,这表示从三个簇到两个簇的过程中合并了一些距离非常远的点。我们在图像上方再次看到这一点,将剩下的两个簇合并为一个簇也需要跨越相对较大的距离。 不幸的是,凝聚聚类仍然无法分离像 two_moons 数据集这样复杂的形状。但我们要学习的下一个算法 DBSCAN 可以解决这个问题。
DBSCAN
聚类算法是 DBSCAN(density-based spatial clustering of applications with noise,即“具有噪声的基于密度的空间聚类应用”)。DBSCAN 的主要优点:不需要用户先验地设置簇的个数,可以划分具有复杂形状的簇,还可以找出不属于任何簇的点。DBSCAN 比凝聚聚类和 k 均值稍慢,但可以扩展到相对较大的数据集。
DBSCAN 的原理是:识别特征空间的“拥挤”区域中的点,在这些区域中许多数据点靠近在一起。这些区域被称为特征空间中的密集(dense)区域。DBSCAN 背后的思想是,簇形成数据的密集区域,并由相对较空的区域分隔开。
在密集区域内的点被称为核心样本(core sample,或核心点)。DBSCAN有两个参数:min_samples 和 eps。如果在距一个给定数据点 eps 的距离内至少有 min_ samples 个数据点,那么这个数据点就是核心样本。DBSCAN将彼此距离小于 eps 的核心样本放到同一个簇中。
算法首先任意选取一个点,然后找到到这个点的距离小于等于 eps 的所有的点。如果距起始点的距离在 eps 之内的数据点个数小于 min_samples,那么这个点被标记为噪声(noise),也就是说它不属于任何簇。如果距离在 eps 之内的数据点个数大于 min_ samples,则这个点被标记为核心样本,并被分配一个新的簇标签。然后访问该点的所有邻居(在距离 eps 以内)。如果它们还没有被分配一个簇,那么就将刚刚创建的新的簇标签分配给它们。如果它们是核心样本,那么就依次访问其邻居,以此类推。簇逐渐增大,直到在簇的 eps 距离内没有更多的核心样本为止。然后选取另一个尚未被访问过的点,并重复相同的过程。
最后,一共有三种类型的点:核心点、与核心点的距离在 eps 之内的点(叫作边界点, boundary point)和噪声。如果DBSCAN算法在特定数据集上多次运行,那么核心点的聚类始终相同,同样的点也始终被标记为噪声。但边界点可能与不止一个簇的核心样本相邻。因此,边界点所属的簇依赖于数据点的访问顺序。一般来说只有很少的边界点,这种对访问顺序的轻度依赖并不重要。
下面我们将DBSCAN应用于演示凝聚聚类的模拟数据集。与凝聚聚类类似,DBSCAN也不允许对新的测试数据进行预测,所以我们将使用fit_predict方法来执行聚类并返回簇标签。
from sklearn.datasets import make_blobs
from sklearn.cluster import DBSCAN
X, y = make_blobs(random_state=0, n_samples=12)
dbscan = DBSCAN()
clusters = dbscan.fit_predict(X)
print("Cluster memberships:\n{}".format(clusters))输出结果:
Cluster memberships:
[-1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1]
如输出结果所见,所有数据点都被分配了标签 -1,这代表噪声。这是 eps 和 min_samples 默认参 数设置的结果,对于小型的玩具数据集并没有调节这些参数。min_samples 和 eps 取不同值时的簇分类我们看下面代码可视化结果:
import matplotlib.pyplot as plt
import mglearn
mglearn.plots.plot_dbscan()
plt.show()输出结果和图形:
min_samples: 2 eps: 1.000000 cluster: [-1 0 0 -1 0 -1 1 1 0 1 -1 -1]
min_samples: 2 eps: 1.500000 cluster: [0 1 1 1 1 0 2 2 1 2 2 0]
min_samples: 2 eps: 2.000000 cluster: [0 1 1 1 1 0 0 0 1 0 0 0]
min_samples: 2 eps: 3.000000 cluster: [0 0 0 0 0 0 0 0 0 0 0 0]
min_samples: 3 eps: 1.000000 cluster: [-1 0 0 -1 0 -1 1 1 0 1 -1 -1]
min_samples: 3 eps: 1.500000 cluster: [0 1 1 1 1 0 2 2 1 2 2 0]
min_samples: 3 eps: 2.000000 cluster: [0 1 1 1 1 0 0 0 1 0 0 0]
min_samples: 3 eps: 3.000000 cluster: [0 0 0 0 0 0 0 0 0 0 0 0]
min_samples: 5 eps: 1.000000 cluster: [-1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1]
min_samples: 5 eps: 1.500000 cluster: [-1 0 0 0 0 -1 -1 -1 0 -1 -1 -1]
min_samples: 5 eps: 2.000000 cluster: [-1 0 0 0 0 -1 -1 -1 0 -1 -1 -1]
min_samples: 5 eps: 3.000000 cluster: [0 0 0 0 0 0 0 0 0 0 0 0]
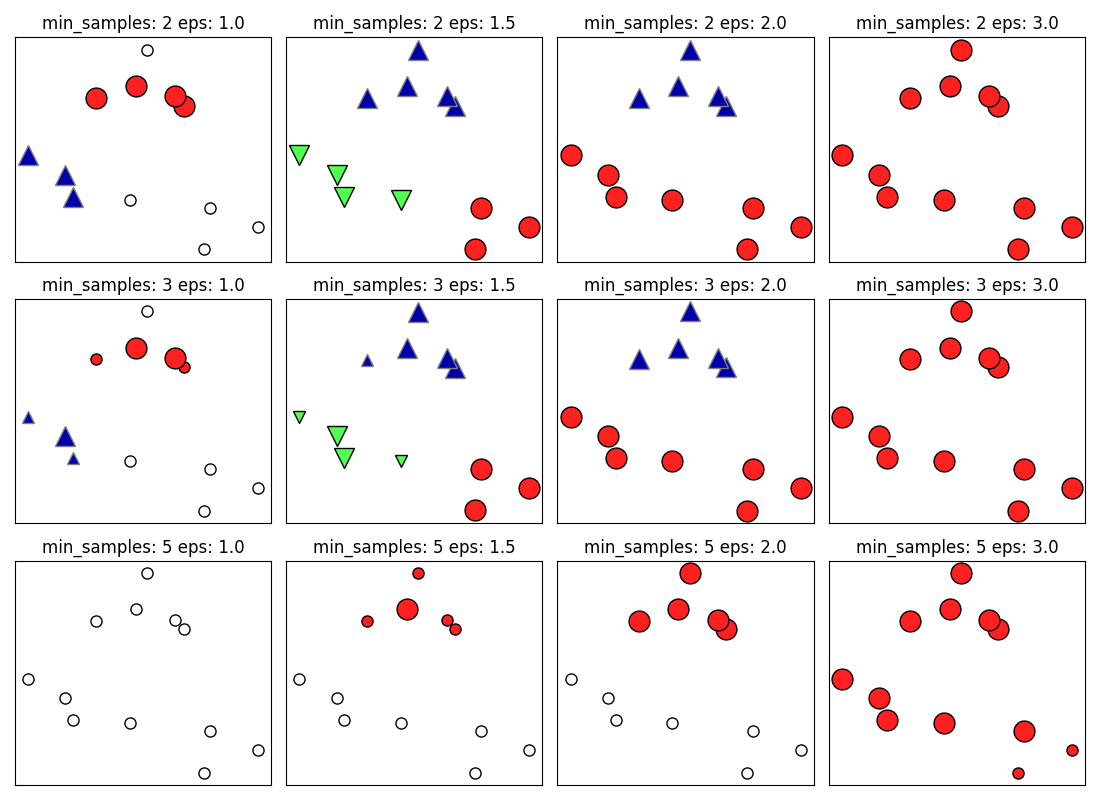
上图是:在 min_samples 和 eps 参数不同取值的情况下,DBSCAN 找到的簇分配。在这张图中,属于簇的点是实心的,而噪声点则显示为空心的。核心样本显示为较大的标记,而边界点则显示为较小的标记。增大 eps(在图中从左到右),更多的点会被包含在一个簇中。这让簇变大,但可能也会导致多个簇合并成一个。增大 min_samples(在图中从上到下),核心点会变得更少,更多的点被标记为噪声。
参数 eps 在某种程度上更加重要,因为它决定了点与点之间“接近”的含义。将 eps 设置得非常小,意味着没有点是核心样本,可能会导致所有点都被标记为噪声。将 eps 设置得非常大,可能会导致所有点形成单个簇。
设置min_samples主要是为了判断稀疏区域内的点被标记为异常值还是形成自己的簇。如果增大 min_samples,任何一个包含少于min_samples个样本的簇现在将被标记为噪声。因此,min_samples 决定簇的最小尺寸。在上图中 eps=1.5 时,从 min_samples=3 到 min_ samples=5,可以清楚地看到这一点。min_samples=3 时有三个簇:一个包含 4 个点,一 个包含 5 个点,一个包含 3 个点。min_samples=5 时,两个较小的簇(分别包含 3 个点和 4 个点)现在被标记为噪声,只保留包含 5 个样本的簇。
虽然 DBSCAN 不需要显式地设置簇的个数,但设置 eps 可以隐式地控制找到的簇的个数。使用 StandardScaler 或 MinMaxScaler 对数据进行缩放之后,有时会更容易找到 eps 的较好取值,因为使用这些缩放技术将确保所有特征具有相似的范围。
下面代码示例展示了在 two_moons 数据集上运行 DBSCAN 的结果。利用默认设置,算法找到了 两个半圆形并将其分开:
import matplotlib.pyplot as plt
import mglearn
from sklearn.datasets import make_moons
from sklearn.cluster import DBSCAN
from sklearn.preprocessing import StandardScaler
X, y = make_moons(n_samples=200, noise=0.05, random_state=0)
# 将数据缩放成平均值为0、方差为1
scaler = StandardScaler()
scaler.fit(X)
X_scaled = scaler.transform(X)
dbscan = DBSCAN()
clusters = dbscan.fit_predict(X_scaled)
# 绘制簇分配
plt.scatter(X_scaled[:, 0], X_scaled[:, 1], c=clusters, cmap=mglearn.cm2, s=60)
plt.xlabel("Feature 0")
plt.ylabel("Feature 1")
plt.show()输出结果:
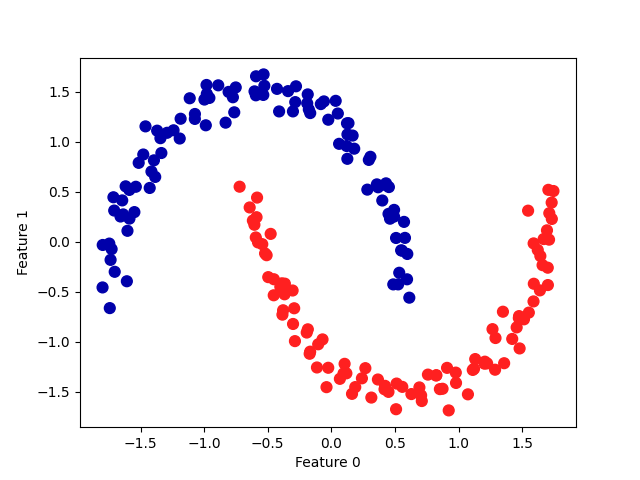
上图是:利用默认值 eps=0.5 的 DBSCAN 找到的簇分配。由于算法找到了我们想要的簇的个数(2个),因此参数设置的效果似乎很好。如果将 eps 减小到 0.2(默认值为 0.5),我们将会得到 8 个簇,这显然太多了。将 eps 增大到 0.7 则会导致只有一个簇。在使用 DBSCAN 时,需要谨慎处理返回的簇分配。如果使用簇标签对另一个数据进行索引,那么使用-1表示噪声可能会产生意料之外的结果。