零、任务介绍
补全carla-ros-bridge/src/ros-bridge/carla_shenlan_projects/carla_shenlan_mpc_controller/src/mpc_controller.cpp中动力学模型和代价函数构造部分,实现车辆MPC控制。
一、环境配置
使用如下命令安装CppAD
sudo apt install cppad
ipopt的安装参考Linux | Ubuntu 20.04安装ipopt和cppAD | 安装全流程+报错解决,使用方法二源码安装即可。
CppAD库的使用可以参考CppAD优化问题求解
二、算法原理
本次使用的线性化模型与上一篇博客自动驾驶控制与规划——Project 3: LQR车辆横向控制的相同。使用欧拉前向法离散化,有如下的等式约束:
x
(
k
+
1
)
=
x
(
k
)
+
v
x
(
k
)
cos
ψ
(
k
)
Δ
t
−
v
y
(
k
)
sin
ψ
(
k
)
Δ
t
y
(
k
+
1
)
=
y
(
k
)
+
v
y
(
k
)
sin
ψ
(
k
)
Δ
t
+
v
y
(
k
)
cos
ψ
(
k
)
Δ
t
ψ
(
k
+
1
)
=
ψ
(
k
)
+
r
(
k
)
Δ
t
v
x
(
k
+
1
)
=
v
x
(
k
)
+
a
x
(
k
)
Δ
t
a
y
(
k
)
=
−
c
f
+
c
r
m
v
x
(
k
)
v
y
(
k
)
+
(
l
r
c
r
−
l
f
c
f
m
v
x
(
k
)
−
v
x
(
k
)
)
r
(
k
)
v
y
(
k
+
1
)
=
v
y
(
k
)
+
a
y
(
k
)
Δ
t
α
(
k
)
=
l
r
c
r
−
l
f
c
f
I
z
v
x
(
k
)
v
y
(
k
)
−
l
f
2
c
f
+
l
r
2
c
r
I
z
v
x
(
k
)
r
(
k
)
r
(
k
+
1
)
=
r
(
k
)
+
α
(
k
)
Δ
t
\begin{aligned} x(k+1) &= x(k) + v_x(k)\cos \psi(k) \Delta t - v_y(k) \sin \psi(k)\Delta t\\ y(k+1) &= y(k) + v_y(k)\sin\psi(k)\Delta t + v_y(k)\cos\psi(k)\Delta t \\ \psi(k+1) &= \psi(k)+r(k)\Delta t \\ v_x(k+1) &= v_x(k) + a_x(k)\Delta t \\ a_y(k) &= -\frac{c_f + c_r}{mv_x(k)} v_y(k) + \left(\frac{l_r c_r - l_f c_f}{m v_x(k)} - v_x(k)\right) r(k) \\ v_y(k+1) &= v_y(k) + a_y(k) \Delta t \\ \alpha(k) &= \frac{l_r c_r - l_f c_f}{I_z v_x(k)} v_y(k) - \frac{l_f^2c_f + l_r^2c_r}{I_z v_x(k)} r(k) \\ r(k+1)&= r(k) + \alpha(k)\Delta t\\ \end{aligned}
x(k+1)y(k+1)ψ(k+1)vx(k+1)ay(k)vy(k+1)α(k)r(k+1)=x(k)+vx(k)cosψ(k)Δt−vy(k)sinψ(k)Δt=y(k)+vy(k)sinψ(k)Δt+vy(k)cosψ(k)Δt=ψ(k)+r(k)Δt=vx(k)+ax(k)Δt=−mvx(k)cf+crvy(k)+(mvx(k)lrcr−lfcf−vx(k))r(k)=vy(k)+ay(k)Δt=Izvx(k)lrcr−lfcfvy(k)−Izvx(k)lf2cf+lr2crr(k)=r(k)+α(k)Δt
其中
x
(
k
)
x(k)
x(k)是
k
k
k时刻车辆在世界系下的
x
x
x坐标;
y
(
k
)
y(k)
y(k)是
k
k
k时刻车辆在世界系下的
y
y
y坐标;
v
x
v_x
vx是车辆纵向速度;
v
y
v_y
vy是车辆横向速度;
ψ
\psi
ψ是偏航角;
r
r
r是偏航角速度;
a
y
a_y
ay是车辆横向加速度;
α
\alpha
α是偏航角加速度;
Δ
t
\Delta t
Δt是预测的时间步长。其他车辆参数含义可以参考上一期博客自动驾驶控制与规划——Project 3: LQR车辆横向控制。
除上述等式约束以外,为了使求解速度加快,增加如下的约束条件令
考虑三个方面的代价函数:
- 误差代价函数:包括纵向速度误差、横向跟踪误差、偏航角误差
- 控制代价函数:包含纵向加速度代价、前轮转角代价
- 平滑代价函数:包含加速度平滑代价、前轮转角平滑代价
J 1 ( k ) = ∑ i = k k + N − 1 ( q c t e e c g 2 ( i ) + q e ψ e ψ 2 ( i ) + q v ( v x ( i ) − v r e f ) 2 ) J 2 ( k ) = ∑ i = k k + N − 1 ( q δ δ 2 ( i ) + q a a x 2 ( i ) ) J 3 ( k ) = ∑ i = k k + N − 2 ( q Δ δ ( δ ( i + 1 ) − δ ( i ) ) 2 + q Δ a ( a x ( i + 1 ) − a ( i ) ) 2 ) \begin{aligned} J_1(k) &= \sum_{i=k}^{k+N-1}\left(q_{cte} e_{cg}^2(i) + q_{e\psi} e_\psi^2(i) + q_v (v_x(i) - v_{ref})^2\right) \\ J_2(k) &= \sum_{i=k}^{k+N-1} \left( q_\delta \delta^2(i) + q_a a_x^2(i)\right) \\ J_3(k)&= \sum_{i=k}^{k+N-2} \left( q_{\Delta\delta} (\delta(i+1) - \delta(i))^2 + q_{\Delta a} (a_x(i+1) - a(i))^2 \right) \end{aligned} J1(k)J2(k)J3(k)=i=k∑k+N−1(qcteecg2(i)+qeψeψ2(i)+qv(vx(i)−vref)2)=i=k∑k+N−1(qδδ2(i)+qaax2(i))=i=k∑k+N−2(qΔδ(δ(i+1)−δ(i))2+qΔa(ax(i+1)−a(i))2)
三、代码实现
构造函数,初始化状态、目标状态、权重等。
FG_eval::FG_eval(const Eigen::VectorXd &state, VectorXd coeffs, const double &target_v, const int &cte_weight, const int &epsi_weight, const int &v_weight, const int &steer_actuator_cost_weight, const int &acc_actuator_cost_weight, const int &change_steer_cost_weight,
const int &change_accel_cost_weight, const int &mpc_prediction_horizon_length, const int &mpc_control_horizon_length, const double &mpc_control_step_length, const double &kinamatic_para_Lf, const double &a_lateral, const double &old_steer_value, const double &old_throttle_value,
const double &steer_ratio) {
this->steer_ratio = steer_ratio;
this->coeffs = coeffs;
this->ref_v = target_v;
this->cte_weight = cte_weight;
this->epsi_weight = epsi_weight;
this->v_weight = v_weight;
this->steer_actuator_cost_weight_fg = steer_actuator_cost_weight;
this->acc_actuator_cost_weight_fg = acc_actuator_cost_weight;
this->change_steer_cost_weight = change_steer_cost_weight;
this->change_accel_cost_weight = change_accel_cost_weight;
this->Np = mpc_prediction_horizon_length;
this->Nc = mpc_control_horizon_length;
this->dt = mpc_control_step_length;
this->Lf = kinamatic_para_Lf;
this->a_lateral = a_lateral;
/*Indexes on the 1-D vector for readability, These indexes are used for "vars"*/
this->x_start = 0;
this->y_start = x_start + Np;
this->psi_start = y_start + Np;
this->v_longitudinal_start = psi_start + Np;
this->v_lateral_start = v_longitudinal_start + Np;
this->yaw_rate_start = v_lateral_start + Np;
this->cte_start = yaw_rate_start + Np;
this->epsi_start = cte_start + Np;
this->front_wheel_angle_start = epsi_start + Np;
this->longitudinal_acceleration_start = front_wheel_angle_start + Nc;
//控制时域长度为25的时候,控制增量一共有24个,第一个时刻点控制量与控制增量相同
// this->front_wheel_angle_increment_start = epsi_start + Np;
// this->longitudinal_acceleration_increment_start = front_wheel_angle_increment_start + Nc - 1;
this->old_steer_value = old_steer_value;
this->old_throttle_value = old_throttle_value;
/* Explicitly gather state values for readability */
this->x = state[0];
this->y = state[1];
this->psi = state[2];
this->v_longitudinal = state[3];
this->v_lateral = state[4];
this->yaw_rate = state[5];
this->cte = state[6];
this->epsi = state[7];
}
FG_eval::operator(),定义MPC的目标函数和约束条件
void FG_eval::operator()(ADvector &fg, ADvector &vars) {
// 部分代码已经给出,请同学们补全
fg[0] = 0; // 0 is the index at which Ipopt expects fg to store the cost value,
/* TODO: Objective term 1: Keep close to reference values.*/
for (size_t t = 0; t < Np; t++) {
fg[0] += cte_weight * CppAD::pow(vars[cte_start + t] - ref_cte, 2);
fg[0] += epsi_weight * CppAD::pow(vars[epsi_start + t] - ref_epsi, 2);
// AD<double> speed = CppAD::sqrt(vars[v_longitudinal_start + t] * vars[v_longitudinal_start + t] + vars[v_lateral_start + t] * vars[v_lateral_start + t]);
// std::cout << "ref_v: " << ref_v << std::endl;
fg[0] += v_weight * CppAD::pow(vars[v_longitudinal_start + t] - ref_v, 2);
}
/* TODO: Objective term 2: Avoid to actuate as much as possible, minimize the use of actuators.*/
for (size_t t = 0; t < Nc; t++) {
fg[0] += steer_actuator_cost_weight_fg * CppAD::pow(vars[front_wheel_angle_start + t], 2);
fg[0] += acc_actuator_cost_weight_fg * CppAD::pow(vars[longitudinal_acceleration_start + t], 2);
}
/* TODO: Objective term 3: Enforce actuators smoothness in change, minimize the value gap between sequential actuation.*/
for (size_t t = 0; t < Nc - 1; t++) {
fg[0] += change_steer_cost_weight * CppAD::pow(vars[front_wheel_angle_start + t + 1] - vars[front_wheel_angle_start + t], 2);
fg[0] += change_accel_cost_weight * CppAD::pow(vars[longitudinal_acceleration_start + t + 1] - vars[longitudinal_acceleration_start + t], 2);
}
/* Initial constraints, initialize the model to the initial state*/
fg[1 + x_start] = vars[x_start];
fg[1 + y_start] = vars[y_start];
fg[1 + psi_start] = vars[psi_start];
fg[1 + v_longitudinal_start] = vars[v_longitudinal_start];
fg[1 + v_lateral_start] = vars[v_lateral_start];
fg[1 + yaw_rate_start] = vars[yaw_rate_start];
fg[1 + cte_start] = vars[cte_start];
fg[1 + epsi_start] = vars[epsi_start];
for (size_t t = 1; t < Np; t++) // 预测模型
{
// Values at time (t),第一次进入该循环的时候,x_0...传入的是给MPC的系统状态的真实值,作为MPC求解的初始条件.
AD<double> x_0 = vars[x_start + t - 1];
AD<double> y_0 = vars[y_start + t - 1];
AD<double> psi_0 = vars[psi_start + t - 1];
AD<double> v_longitudinal_0 = vars[v_longitudinal_start + t - 1] + 0.00001;
AD<double> v_lateral_0 = vars[v_lateral_start + t - 1];
AD<double> yaw_rate_0 = vars[yaw_rate_start + t - 1];
AD<double> cte_0 = vars[cte_start + t - 1];
AD<double> epsi_0 = vars[epsi_start + t - 1];
// Values at time (t+1)
AD<double> x_1 = vars[x_start + t];
AD<double> y_1 = vars[y_start + t];
AD<double> psi_1 = vars[psi_start + t];
AD<double> v_longitudinal_1 = vars[v_longitudinal_start + t] + 0.00001;
AD<double> v_lateral_1 = vars[v_lateral_start + t];
AD<double> yaw_rate_1 = vars[yaw_rate_start + t];
AD<double> cte_1 = vars[cte_start + t];
AD<double> epsi_1 = vars[epsi_start + t];
// Only consider the actuation at time t.
AD<double> front_wheel_angle_0;
AD<double> longitudinal_acceleration_0;
front_wheel_angle_0 = vars[front_wheel_angle_start + t - 1];
longitudinal_acceleration_0 = vars[longitudinal_acceleration_start + t - 1];
// reference path
AD<double> f_0 = coeffs[0] + coeffs[1] * x_0 + coeffs[2] * CppAD::pow(x_0, 2) + coeffs[3] * CppAD::pow(x_0, 3) + coeffs[4] * CppAD::pow(x_0, 4) + coeffs[5] * CppAD::pow(x_0, 5); // + coeffs[6] * CppAD::pow(x_0, 6);
// reference psi: can be calculated as the tangential angle of the polynomial f evaluated at x_0
AD<double> psi_des_0 = CppAD::atan(1 * coeffs[1] + 2 * coeffs[2] * x_0 + 3 * coeffs[3] * CppAD::pow(x_0, 2) + 4 * coeffs[4] * CppAD::pow(x_0, 3) + 5 * coeffs[5] * CppAD::pow(x_0, 4)); // + 6 * coeffs[6] * CppAD::pow(x_0, 5));
// TODO: 补全车辆动力学模型,作为MPC的等式约束条件,车辆动力学模型需要注意参数的正方向的定义
/*The idea here is to constraint this value to be 0.*/
/* 全局坐标系 */
fg[1 + x_start + t] = x_1 - (x_0 + (v_longitudinal_0 * CppAD::cos(psi_0) - v_lateral_0 * CppAD::sin(psi_0)) * dt);
fg[1 + y_start + t] = y_1 - (y_0 + (v_longitudinal_0 * CppAD::sin(psi_0) + v_lateral_0 * CppAD::cos(psi_0)) * dt);
/* 航向角变化 */
fg[1 + psi_start + t] = psi_1 - (psi_0 + yaw_rate_0 * dt);
/* 车辆纵向速度 */
fg[1 + v_longitudinal_start + t] = v_longitudinal_1 - (v_longitudinal_0 + longitudinal_acceleration_0 * dt);
/* 车辆侧向速度 */
// 注意这里front_wheel_angle_0符号和第四章推导中定义的delta方向相反
AD<double> a_lateral = -2 * (Cf + Cr) / (m * v_longitudinal_0) * v_lateral_0 + (2 * (lr * Cr - lf * Cf) / (m * v_longitudinal_0) - v_longitudinal_0) * yaw_rate_0 - 2 * Cf / m * front_wheel_angle_0;
fg[1 + v_lateral_start + t] = v_lateral_1 - (v_lateral_0 + a_lateral * dt);
/* 车辆横摆角速度 */
AD<double> yaw_acceleration = 2 * (lr * Cr - lf * Cf) / (I * v_longitudinal_0) * v_lateral_0 - 2 * (lf * lf * Cf + lr * lr * Cr) / (I * v_longitudinal_0) * psi_0 - 2 * lf * Cf / I * front_wheel_angle_0;
fg[1 + yaw_rate_start + t] = yaw_rate_1 - (yaw_rate_0 + yaw_acceleration * dt);
/* 横向位置跟踪误差 */
fg[1 + cte_start + t] = cte_1 - (f_0 - y_0 + v_longitudinal_0 * CppAD::tan(epsi_0) * dt);
/* 航向跟踪误差 */
fg[1 + epsi_start + t] = epsi_1 - (psi_0 - psi_des_0 - v_longitudinal_0 * (front_wheel_angle_0 / 1) / Lf * dt);
}
}
mpc_controller::Solve求解MPC优化问题,返回最优控制量以及预测的状态轨迹。
std::vector<double> mpc_controller::Solve(const Eigen::VectorXd &state, const Eigen::VectorXd &coeffs, const double &target_v, const int &cte_weight, const int &epsi_weight, const int &v_weight, const int &steer_actuator_cost_weight, const int &acc_actuator_cost_weight,
const int &change_steer_cost_weight, const int &change_accel_cost_weight,
// const int &mpc_prediction_horizon_length,
const int &mpc_control_horizon_length, const double &mpc_control_step_length, const double &kinamatic_para_Lf, const double &a_lateral, const double &old_steer_value, const double &old_throttle_value, const double &steer_ratio) {
this->Nc = mpc_control_horizon_length;
this->Np = Nc + 1;
this->x_start = 0;
this->y_start = x_start + Np;
this->psi_start = y_start + Np;
this->v_longitudinal_start = psi_start + Np;
this->v_lateral_start = v_longitudinal_start + Np;
this->yaw_rate_start = v_lateral_start + Np;
this->cte_start = yaw_rate_start + Np;
this->epsi_start = cte_start + Np;
this->front_wheel_angle_start = epsi_start + Np;
this->longitudinal_acceleration_start = front_wheel_angle_start + Nc; //控制时域长度为25的时候,控制量一共有24个。
// this->front_wheel_angle_increment_start = epsi_start + Np;
// this->longitudinal_acceleration_increment_start = front_wheel_angle_increment_start + Nc - 1;
this->a_lateral = a_lateral;
bool ok = true;
typedef CPPAD_TESTVECTOR(double) Dvector;
/* Explicitly gather state values for readability */
double x = state[0];
double y = state[1];
double psi = state[2];
double v_longitudinal = state[3];
double v_lateral = state[4];
double yaw_rate = state[5];
double cte = state[6];
double epsi = state[7];
/* Set the number of model variables (includes both states and inputs). */
/* 系统状态量 + 系统控制增量 */
size_t n_vars = Np * 8 + Nc * 2;
/* Set the number of contraints */
size_t n_constraints = Np * 8;
/* Initialize all of independent variables to zero. */
Dvector vars(n_vars);
for (size_t i = 0; i < n_vars; i++) {
vars[i] = 0.0;
}
// Set the initial variable values**初始化变量及变量上下限**
vars[x_start] = x;
vars[y_start] = y;
vars[psi_start] = psi;
vars[v_longitudinal_start] = v_longitudinal;
vars[v_lateral_start] = v_lateral;
vars[yaw_rate_start] = yaw_rate;
vars[cte_start] = cte;
vars[epsi_start] = epsi;
Dvector vars_lower_bounds(n_vars);
Dvector vars_upper_bounds(n_vars);
/* Set limits for non-actuators (avoid numerical issues during optimization). */
for (size_t i = 0; i < front_wheel_angle_start; i++) {
vars_lower_bounds[i] = -std::numeric_limits<float>::max();
vars_upper_bounds[i] = +std::numeric_limits<float>::max();
}
/* Set upper and lower constraints for steering. */
double max_degree = 24;
double max_radians = max_degree * M_PI / 180;
for (size_t i = front_wheel_angle_start; i < longitudinal_acceleration_start; i++) {
vars_lower_bounds[i] = -max_radians;
vars_upper_bounds[i] = +max_radians;
}
/* Set uppper and lower constraints for acceleration. */
double max_acceleration_value = 1.0;
for (size_t i = longitudinal_acceleration_start; i < n_vars; i++) {
vars_lower_bounds[i] = -max_acceleration_value;
vars_upper_bounds[i] = +max_acceleration_value;
}
/* Initialize to zero lower and upper limits for the constraints*/
Dvector constraints_lower_bounds(n_constraints);
Dvector constraints_upper_bounds(n_constraints);
for (size_t i = 0; i < n_constraints; i++) {
constraints_lower_bounds[i] = 0;
constraints_upper_bounds[i] = 0;
}
/* Force the solver to start from current state in optimization space. */
/* 约束条件的形式为 [x(0); x(1) = f(x(0)); ... x(N) = f(x(N-1)); , 每一个约束的第一项其实就是系统当前状态,所以直接约束该量的第一项。
不能直接给状态 vars 的第一项赋值来限制求解起点,因为状态和控制量理论上都是自由的,所以这里通过设置约束条件第一项的方式来指定优化求解起点,从而加速求解。*/
constraints_lower_bounds[x_start] = x;
constraints_lower_bounds[y_start] = y;
constraints_lower_bounds[psi_start] = psi;
constraints_lower_bounds[v_longitudinal_start] = v_longitudinal;
constraints_lower_bounds[v_lateral_start] = v_lateral;
constraints_lower_bounds[yaw_rate_start] = yaw_rate;
constraints_lower_bounds[cte_start] = cte;
constraints_lower_bounds[epsi_start] = epsi;
constraints_upper_bounds[x_start] = x;
constraints_upper_bounds[y_start] = y;
constraints_upper_bounds[psi_start] = psi;
constraints_upper_bounds[v_longitudinal_start] = v_longitudinal;
constraints_upper_bounds[v_lateral_start] = v_lateral;
constraints_upper_bounds[yaw_rate_start] = yaw_rate;
constraints_upper_bounds[cte_start] = cte;
constraints_upper_bounds[epsi_start] = epsi;
/* Object that computes objective and constraints. */
FG_eval fg_eval(state, coeffs, target_v, cte_weight, epsi_weight, v_weight, steer_actuator_cost_weight, acc_actuator_cost_weight, change_steer_cost_weight, change_accel_cost_weight, Np, Nc, mpc_control_step_length, kinamatic_para_Lf, a_lateral, old_steer_value, old_throttle_value, steer_ratio);
/* NOTE: You don't have to worry about these options. options for IPOPT solver. */
std::string options;
/* Uncomment this if you'd like more print information. */
options += "Integer print_level 0\n";
/* NOTE: Setting sparse to true allows the solver to take advantage
of sparse routines, this makes the computation MUCH FASTER. If you can
uncomment 1 of these and see if it makes a difference or not but if you
uncomment both the computation time should go up in orders of magnitude. */
options += "Sparse true forward\n";
options += "Sparse true reverse\n";
/* NOTE: Currently the solver has a maximum time limit of 0.5 seconds. */
/* Change this as you see fit. */
options += "Numeric max_cpu_time 0.5\n"; // 单位:s
/* Place to return solution. */
CppAD::ipopt::solve_result<Dvector> solution;
/* Solve the problem. */
// cout << "Solve the problem......" << endl;
CppAD::ipopt::solve<Dvector, FG_eval>(options, vars, vars_lower_bounds, vars_upper_bounds, constraints_lower_bounds, constraints_upper_bounds, fg_eval, solution);
/* Check some of the solution values. */
ok &= solution.status == CppAD::ipopt::solve_result<Dvector>::success;
/* Cost! */
// auto cost = solution.obj_value;
// std::cout << "Cost: " << cost << std::endl;
/* Return the first actuator values. The variables can be accessed with 'solution.x[i]'. */
std::vector<double> result;
result.clear();
// cout << solution.x << endl;
// cout << front_wheel_angle_start << endl;
result.push_back(solution.x[front_wheel_angle_start]);
result.push_back(solution.x[longitudinal_acceleration_start]);
/* Add 'future' solutions (where MPC is going). */
for (size_t i = 0; i < Np - 1; i++) {
result.push_back(solution.x[x_start + i]);
result.push_back(solution.x[y_start + i]);
}
// std::cout << "end now" << std::endl;
return result;
}
代价的权重:
# MPC 目标函数里面可以调节的权重
mpc_cte_weight_int: 600 # ok
mpc_epsi_weight_int: 1000 # ok
mpc_v_weight_int: 200 # ok real 100
# 控制量幅值代价权重
mpc_steer_actuator_cost_weight_int: 400 # ok
mpc_acc_actuator_cost_weight_int: 100 # ok
# 前后两次控制量变化的代价权重
mpc_change_steer_cost_weight_int: 200 # ok
mpc_change_accel_cost_weight_int: 200 # ok
四、效果展示
实验过程中发现在相同的权重下,给定不同的求解时间,会对MPC的性能产生较大的影响:
options += "Numeric max_cpu_time 0.5\n"; // 单位:s
求解时间为0.5s的效果,计时发现求解一次的时间在50ms左右,但是有时会到200-300ms,跟踪效果良好,无振荡。
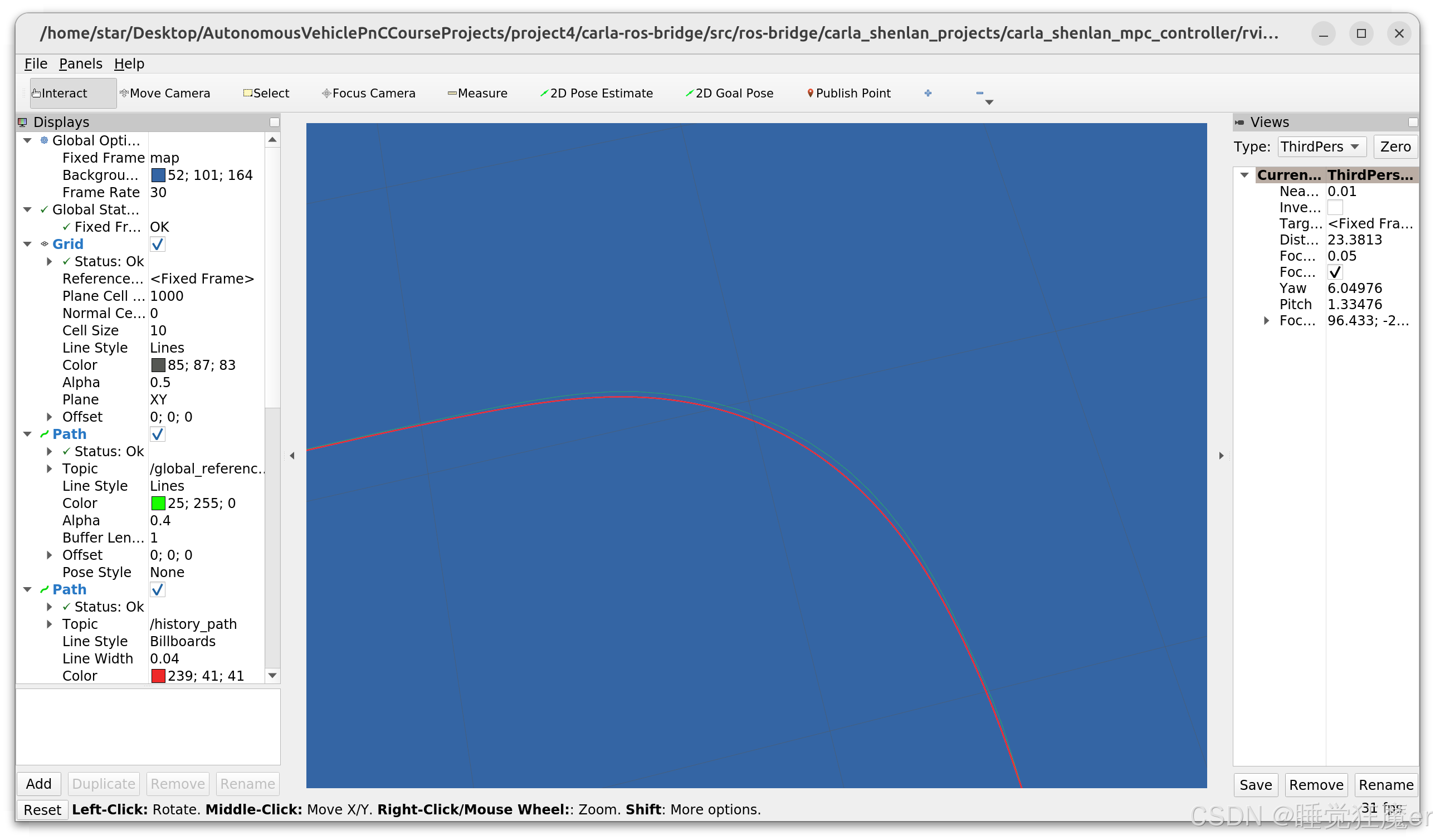
求解时间为0.2s的效果,求解时间在50ms左右,最大求解时间被限制在200ms左右。
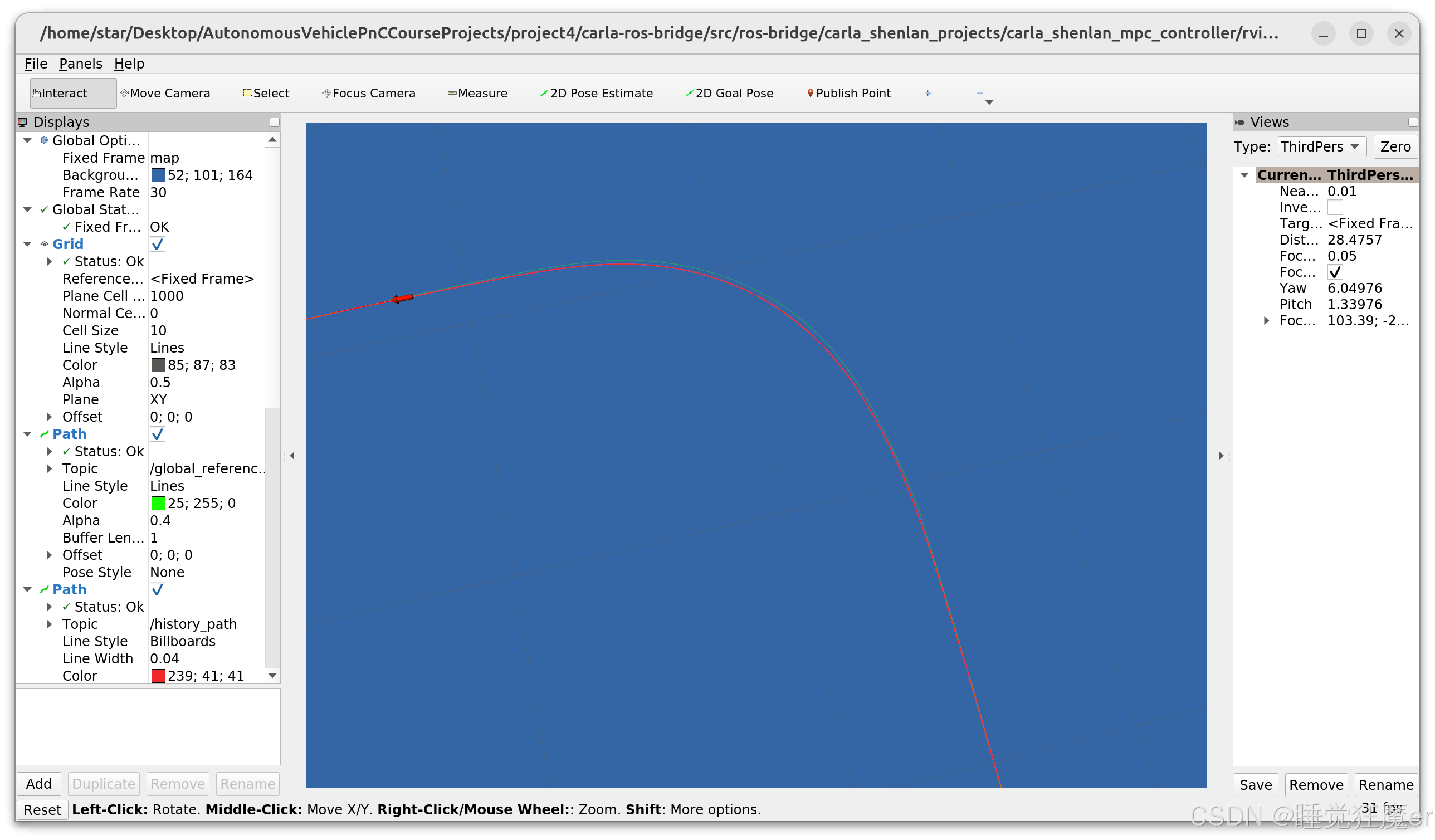
跟踪直线轨迹时出现了轻微振荡。
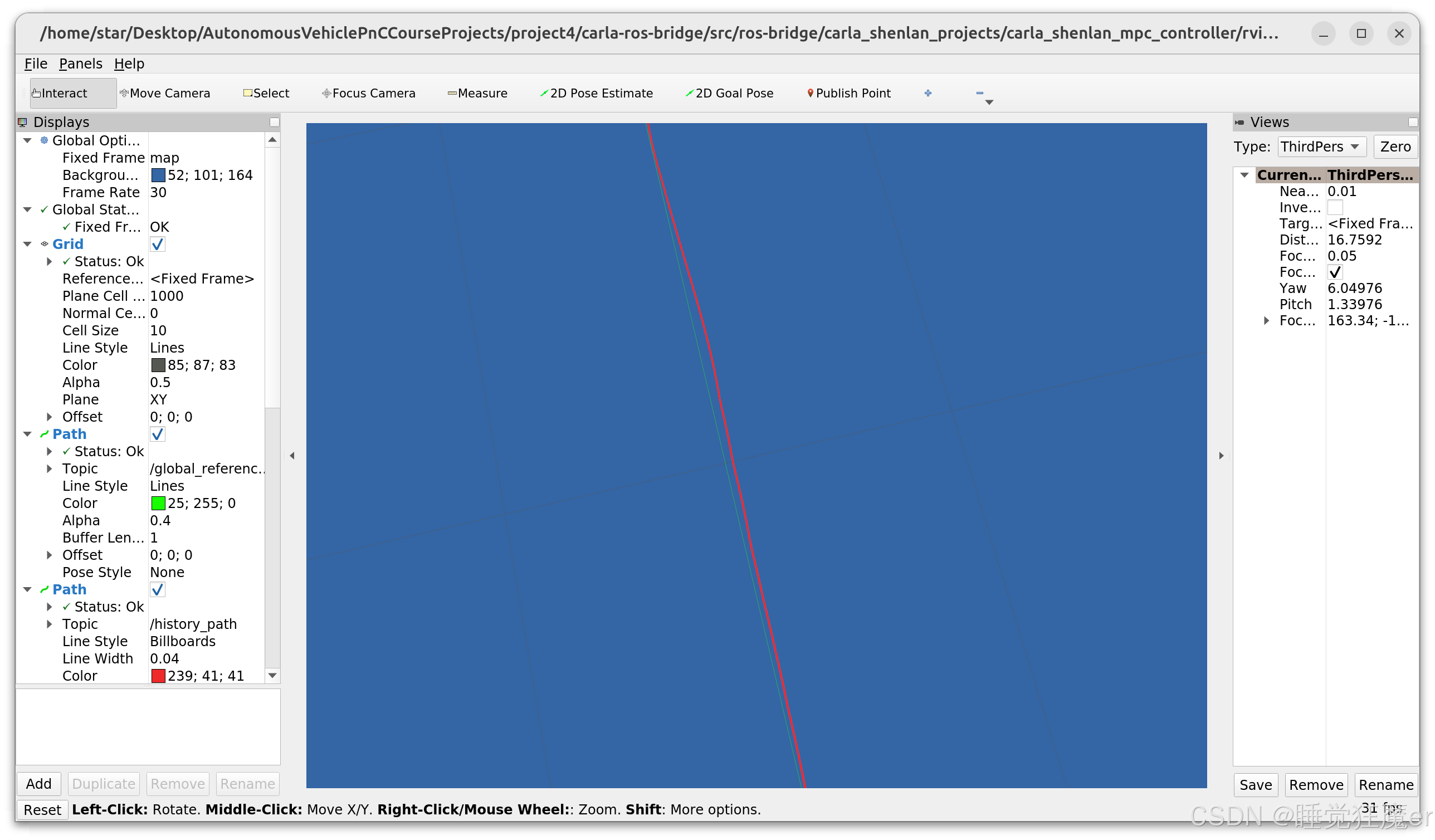
求解时间为0.05s的效果,最大求解时间被限制在50ms-70ms之间。
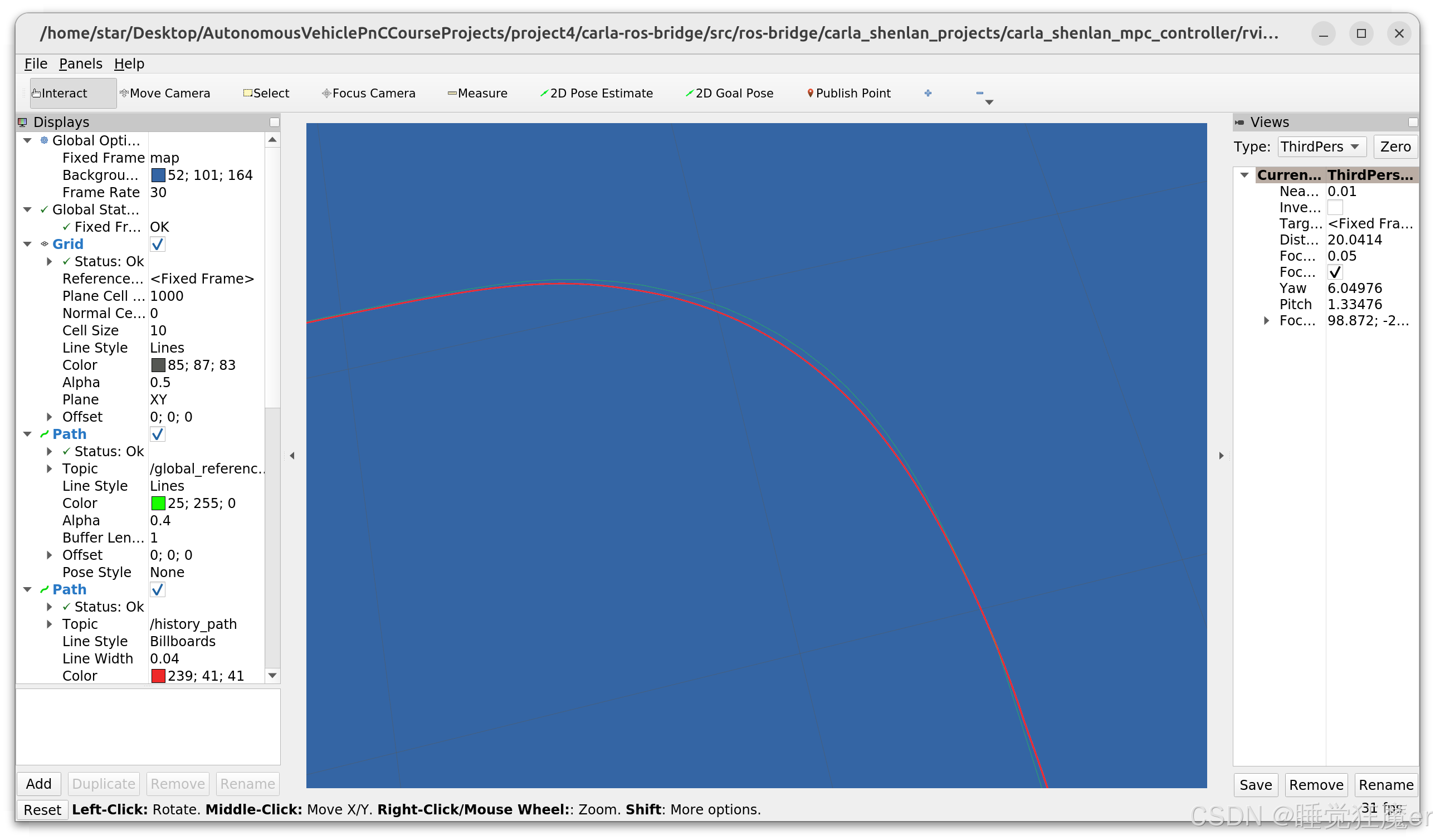
跟踪直线轨迹时出现明显振荡:
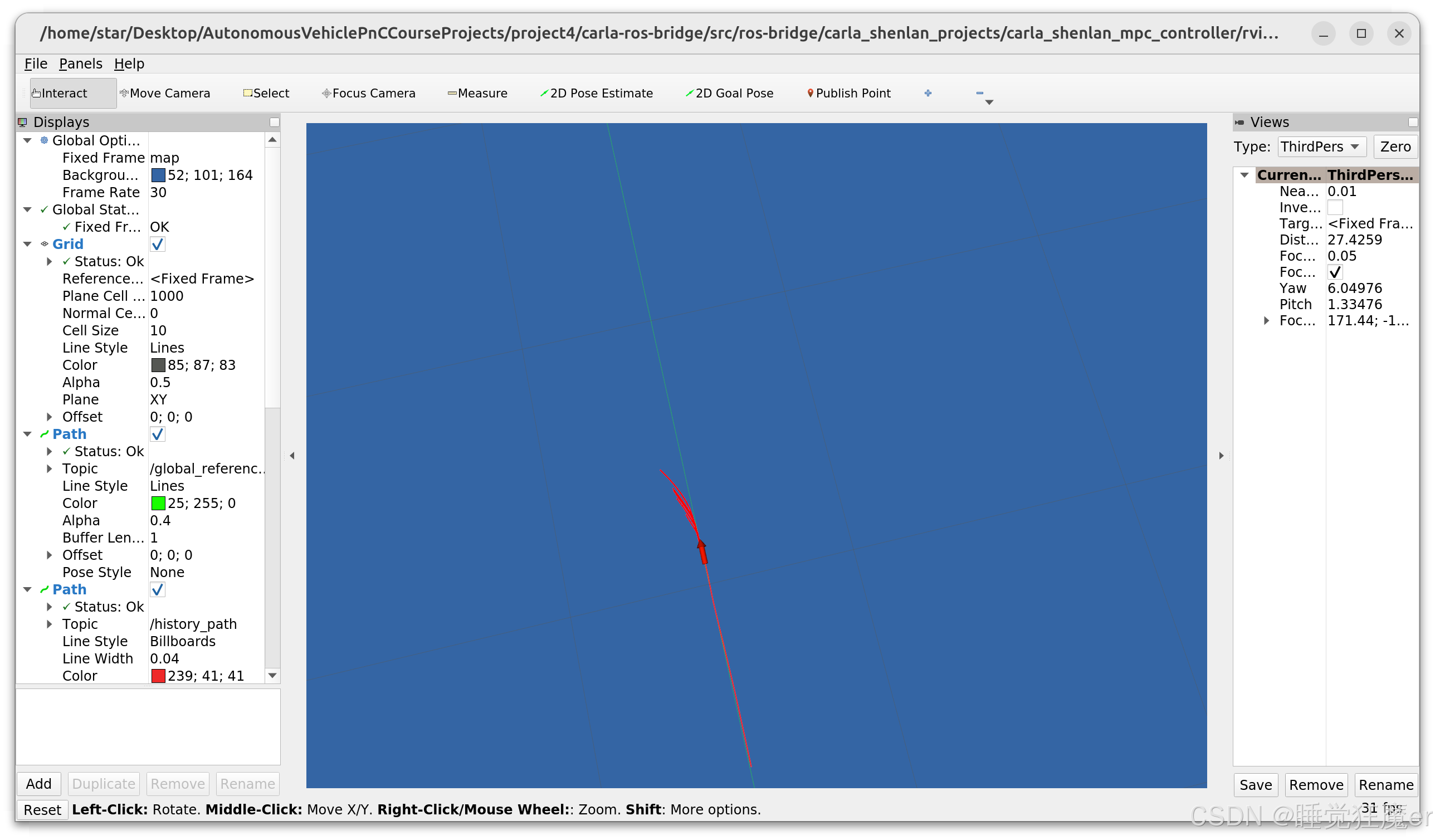
实际工程实现中,需要权衡求解精度与实时性,应当通过实验和工程约束确定最大求解时间等参数。
自动驾驶控制与规划——Project 4: MPC车辆控制