SparkGraphX讲解
1、为何使用SparkGraphiX图处理?
许多大数据以大规模图或网络的形式呈现,尤其是许多的非图结构的大数据,常会被转换为图模型进行分析。
图数据结构能够很好地表达数据之间的关联性。
2、图——基本术语认知
概念:图是由顶点集合(vertex)及顶点间的关系集合(边edge)组成的一种网状数据结构,可以对事物之间的关系建模。通常表示为二元组:Graph =(V,E)
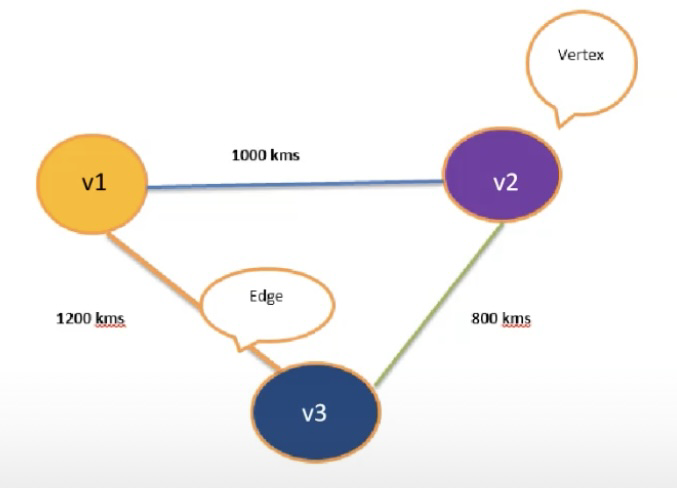
图中基本知识点:
- 图可以分为有向图,无向图,有环图,无环图等。
-
度:指与这个顶点相关联的边的数量
对于有向图而言:
- 出度:指从当前顶点指向其他顶点的边的数量
入度:其他顶点指向当前顶点的边的数量 - 度 = 出度+入度
- 出度:指从当前顶点指向其他顶点的边的数量
3、SparkGraphX简介
3.1:基本概念
Spark GraphX 是一个分布式图处理框架,为图计算和图挖掘提供了简洁易用且丰富多彩的接口。
3.2:Graph X 特点
-
基于内存实现了数据的复用与快速读取。
-
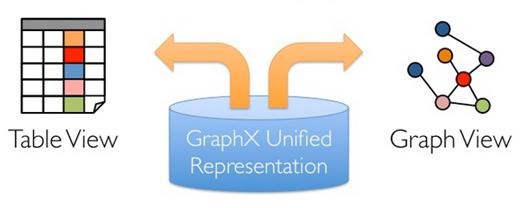
Resilient Distributed Property Graph(弹性分布式属性图):
通过弹性分布式属性图统一了图视图(Graph)与表视图(Table)
-
GraphX的核心抽象是Resilient Distributed Property Graph(弹性分布式属性图),是一种顶点和边都带属性的有向多重图。
-
其扩展了Spark RDD的抽象,一份物理存储,两种视图(Table和Graph)
-
两种视图都有自己独有的操作符,从而获得了灵活操作和执行效率。
-
-
GraphX能与Spark Streaming、Spark sql 和 Spark MLib等无缝衔接
3.3:Graph X中有重要的概念
(1)Vertices(顶点):对应的RDD名称为VertexRDD【RDD[Vertex]】,包括顶点ID(VertexId)和顶点属性(VD,Vertex Data)
(2)Edges(边):对应的RDD名称为EdgeRDD【RDD[Edge[(String,Int)]]】,包括源顶点ID(srcId)、目标顶点ID(dstId)和边属性(ED,Edge Data)
(3)Triplets(三元组):对应的是关系RDD【RDD[EdgeTriplet]】,包括源顶点ID【srcId:VertexId】、源顶点属性【srcAttr:(String,Int,String)】、边属性【attr:(String,Int)】、目标顶点ID【dstId:VertexId】、目标顶点属性【dstAttr:(String,Int,String)】

(4)度(Degree):包括inDegrees(每个顶点入度)、outDegrees(每个顶点的出度)、degrees(每个顶点的度)
3.4:存储模式——分区切割策略
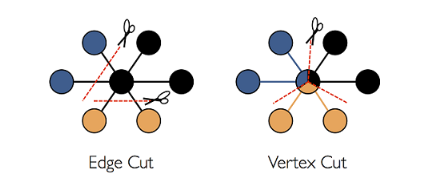
分区切割策略(PartitionStrategy):
1、EdgeCut => 保证点在同一分区
EdgePartition1D => 同点边(出入度)同分区
EdgePartition2D => 邻接矩阵:与顶点关联的边最多被分配到(2 * sqrt(分区总数))个分区中
2、VertexCut => 保证边在同一分区(Spark优选切割策略,因为边较为复杂)
RandomVertexCut => 两同点同方向(同边)同分区
CanonicalRandomVertexCut => 两同点边同分区
4、常用API
class Graph[VD,ED]{
// 图信息
val numEdges: Long // 边数
val numVertices: Long // 点数
val inDegrees: VertexRDD[Int] // 入度
val outDegrees: VertexRDD[Int] // 出度
val degrees: VertexRDD[Int] // 度数
// 属性算子
def mapVertices[VD2](map: (VertexId, VD) => VD2): Graph[VD2, ED]
def mapEdges[ED2](map: Edge[ED] => ED2): Graph[VD, ED2]
def mapTriplets[ED2](map: EdgeTriplet[VD, ED] => ED2): Graph[VD, ED2]
// 结构算子
def reverse: Graph[VD, ED]
def subgraph(epred: EdgeTriplet[VD,ED] => Boolean,
vpred: (VertexId, VD) => Boolean): Graph[VD, ED]
// 关联算子
def joinVertices[U](table: RDD[(VertexId, U)])(map: (VertexId, VD, U) => VD)
: Graph[VD, ED]
def outerJoinVertices[U, VD2]
(table: RDD[(VertexId, U)])
(map: (VertexId, VD, Option[U]) => VD2)
: Graph[VD2, ED]
}
class GraphOps[VD, ED](graph : org.apache.spark.graphx.Graph[VD, ED]){
// 👉同分区👈内相同边(顶点ID顺序值都相同)合并
def groupEdges(merge : scala.Function2[ED, ED, ED]) :
org.apache.spark.graphx.Graph[VD, ED]
}
5、算法
页面等级(Page Rank)
用于评估网页链接的质量和数量,以确定该网页的重要性和权威性的相对分数,范围为0到10
从本质上讲,Page Rank是找出图中顶点(网页链接)的重要性(值越大越重要)过程简单讲解:尽可能的在分散的点中选取几个,然后这几个点进行拉取周围的点形成多个圈,在这几个圈内部会去寻找绝对中心点。依次类推,达到tol阈值时会停止迭代。
def pageRank( tol : scala.Double, // 收敛最小误差,越小越好,确定迭代是否结束的参数 resetProb : scala.Double // 随机【重复概率】 ) : org.apache.spark.graphx.Graph[scala.Double, scala.Double]案列:顶点质量
graph.pageRank(0.0001,0.2) .vertices .foreach(println) ----------------------------- (1,0.6533816355047241) (4,0.5437786042062481) (6,0.8615213520717165) (3,1.2889169066237742) (2,1.0530712359694594) (5,1.5993302656240773) -----------------------------
三角数量
计算经过每个顶点的三角形数量
用于评估:社区、团体、机构、组织内部关系的紧密程度或稳定性,三角形越少越松散def triangleCount() : org.apache.spark.graphx.Graph[scala.Int, ED]案例:稳定性
graph.triangleCount() .vertices .foreach(println) // (顶点id,参与的三角形数量) ------------------------- (3,5) (1,7) (5,5) (6,3) (2,3) (4,7) -------------------------
连通分量
连通分量是一个子图,其中任何两个顶点通过一条边或一系列边相互连接,其顶点是原始图顶点集的子集,其边是原始图边集的子集
用于反应图中顶点间的连通性
def connectedComponents() : org.apache.spark.graphx.Graph[org.apache.spark.graphx.VertexId, ED] def stronglyConnectedComponents(numIter : scala.Int) : org.apache.spark.graphx.Graph[org.apache.spark.graphx.VertexId, ED]案例:
// 强连通图(每两个顶点之间都存在路径) graph.connectedComponents() .vertices .foreach(println) ----------------------------- (5,1) // 顶点 5 属于连通分量 1 (4,1) // 顶点 4 属于连通分量 1 (1,1) // 顶点 1 属于连通分量 1 (2,1) // 顶点 2 属于连通分量 1 (3,1) // 顶点 3 属于连通分量 1 (6,1) // 顶点 6 属于连通分量 1 -----------------------------
PREGEL
是Google提出的用于大规模分布式图计算框架
- 图遍历(BFS)
- 单源最短路径(SSSP)
- Page Rank计算
Pregel的计算由一系列迭代组成,称为 super steps
- 每个顶点从上一个 super step 接收入站消息
- 计算顶点新的属性值
- 在下一个 super step 中向相邻的顶点发送消息
- 当没有剩余消息时,迭代结束
def pregel[A]( initialMsg: A, maxIterations: Int, activeDirection: EdgeDirection )( vprog: (VertexID, VD, A) => VD, sendMsg: EdgeTriplet[VD, ED] => Iterator[(VertexID,A)], mergeMsg: (A, A) => A ) : Graph[VD, ED]案例:求最短路径(srcId为1L,到其他点的最短路径)
// 1、初始化操作 val srcId = 1L // 初始化(点):对顶点重新定义(VertexId,Distance),保留边 // 除了 srcId本身点是(1,0),其他点为(VertexId,2100000000) val initialVertices: Graph[Long, Int] = graph.mapVertices({ // 点重新定义,边依旧是原来的边 // 偏函数+模式匹配 case (vertexId, t2) if (vertexId == srcId) => 0L // 若指向自己,则为0 case _ => Long.MaxValue // 指向其他人距离为最大值 }) // 2、生成结果图 val vertexCount: Int = initialVertices.vertices.count().toInt val rstGraph: Graph[Long, Int] = initialVertices.pregel[Long]( Int.MaxValue, // 初始化值 vertexCount, // 最大迭代次数(按照顶点数量) EdgeDirection.Out )( // 初始化:每一轮迭代初始化节点值 // VD:上一轮计算的值, A:新值 (VertexId, VD, A) => { val min: Long = Math.min(VD, A) println(s"$VertexId ($VD,$A) = $min") min }, // 发送消息:EdgeTriplet(srcId,srcAttr,attr,dstId,dstAttr) e => { // (VertexId,距离) // srcAttr:前一个顶点的距离 -- attr:边长 --> dstAttr:后一个顶点的距离 // srcAttr + attr < dstAttr 则发消息进行替换,否则不发送消息 val distance: Long = e.srcAttr + e.attr if (distance < e.dstAttr) { // 发送消息进行替换 println(s"sendMsg from ${e.srcId} to ${e.dstId} for ($distance,${e.dstAttr}) = $distance") Iterator((e.dstId, distance)) } else { // 不发消息 Iterator.empty } }, // 合并 (a, b) => { val min: Long = Math.min(a, b) println(s"merge($a,$b),最终选择$min") min } ) rstGraph.vertices.foreach(println) // (到xx点,距离) ---------------------------------- (2,1) (4,3) (5,5) (6,2) (1,0) (3,3) ----------------------------------
6、应用场景
在地图应用中寻找最短路径
社交网络关系
网页间超链接关系
7、小型案例
7.1.准备工作
数据模拟
import scala.collection.mutable.ArrayBuffer
import scala.collection.mutable.Set
import scala.util.Random
import scala.util.control.Breaks.{breakable,break}
val buffer:ArrayBuffer[Edge[Int]] = ArrayBuffer()
val rand = new Random()
val array = Array(1L,2L,3L,4L,5L,6L) // 六个点
val set:Set[(Long,Long)] = Set() // 去重
var cnt = 0
while(cnt<21){
array.foreach(one=>{ // 点1
breakable({
while (true){
val two = array(rand.nextInt(array.size)) // 点2
if(one != two){
val relation = (one,two) // 构成关系
if(!set.contains(relation)){
buffer.append(Edge(relation._1,relation._2,rand.nextInt(6)))
set.add(relation)
cnt += 1
break() // 跳出循环
}
}
}
})
})
}
------------- 输出结果形式 ------------
Edge(1,5,0)
Edge(2,1,2)
Edge(3,6,3)
Edge(4,2,1)
Edge(5,2,4)
-------------------------------------
创建图对象
// 边数据:描述点与点间关系【有方向】
val es = Seq(
Edge(1L,6L,4),
Edge(1L,6L,4),
Edge(2L,5L,4),
Edge(3L,6L,4),
Edge(4L,5L,3),
Edge(5L,1L,5),
Edge(6L,2L,5),
//Edge(5L,1L,5),
//Edge(6L,2L,5),
Edge(1L,5L,1),
Edge(2L,3L,2),
Edge(3L,4L,0),
Edge(4L,2L,4),
Edge(5L,2L,4),
//Edge(2L,3L,2),
Edge(6L,5L,3),
Edge(1L,2L,1),
Edge(2L,1L,0),
Edge(3L,5L,3),
//Edge(6L,5L,3),
Edge(4L,6L,0),
//Edge(2L,1L,0),
Edge(5L,3L,0),
Edge(6L,3L,4),
Edge(1L,3L,5),
Edge(2L,6L,1),
Edge(3L,1L,1),
//Edge(2L,6L,1),
//Edge(3L,1L,1),
Edge(4L,1L,5),
Edge(5L,6L,3),
//Edge(5L,6L,3),
Edge(6L,1L,3)
)
// 点数据
val vs = Seq(
(1L,("jack",22)),
(2L,("pola",12)),
(3L,("mike",26)),
(4L,("wang",17)),
(5L,("liu",19)),
(6L,("frimiku",18)),
)
val conf: SparkConf = new SparkConf()
.setAppName("graphx-01")
.setMaster("local[4]")
val sc = new SparkContext(conf)
// 点:描述的是人信息(L来表示点)
val vertex: RDD[(Long, (String, Int))] = sc.makeRDD(vs)
// 边
val edge: RDD[Edge[Int]] = sc.makeRDD(es)
// 构建图 (源码 => 基础:Graph,高阶:GraphOps)
val graph: Graph[(String, Int), Int] = Graph(vertex, edge)
7.2.实际演示
遍历
// 1、查看所有顶点
graph.vertices.foreach(println)
-----------------------------
(1,(jack,22))
(2,(pola,12))
(4,(wang,17))
(3,(mike,26))
(5,(liu,19))
(6,(frimiku,18))
-----------------------------
// 2、查看所有的边【简略】
graph.edges.foreach(println)
-----------------------------
Edge(4,6,0)
Edge(4,1,5)
Edge(1,2,1)
Edge(1,3,5)
-----------------------------
// 3、查看所有的边(将点带入)【完整】
graph.triplets.foreach(println)
------------------------------------
((5,(liu,19)),(6,(frimiku,18)),3)
((4,(wang,17)),(5,(liu,19)),3)
((3,(mike,26)),(4,(wang,17)),0)
((4,(wang,17)),(2,(pola,12)),4)
------------------------------------
// 4、入度:指向自己的个数
graph.inDegrees.foreach(println) // (id,入度)
---------------------------
(4,1)
(3,4)
(2,4)
(5,5)
(6,5)
(1,5)
---------------------------
// 5、出度:指向别人的个数
graph.outDegrees.foreach(println) // (id,出度)
---------------------------
(6,4)
(5,4)
(3,4)
(4,4)
(1,4)
(2,4)
---------------------------
// 4,5组合:将入度和出度一起显示
graph
.inDegrees
.join(graph.outDegrees)
.foreach(println) // (id,(入度,出度))
---------------------------
(4,(1,4))
(3,(4,4))
(2,(4,4))
(1,(5,4))
(6,(5,4))
(5,(5,4))
---------------------------
// 6、度:入度+出度
graph.degrees.foreach(println)
---------------------------
(3,8)
(4,5)
(5,9)
(6,9)
(2,8)
(1,9)
---------------------------
案例一:长一岁
// 长一岁:每个顶点中的人物的年龄长一岁
graph.mapVertices((id,t2)=>(id,(t2._1,t2._2+1))) // (id,(名字,年龄))
.vertices
.foreach(println)
--------------------------
(5,(5,(liu,20)))
(4,(4,(wang,18)))
(6,(6,(frimiku,19)))
(1,(1,(jack,23)))
(2,(2,(pola,13)))
(3,(3,(mike,27)))
--------------------------
案例二:找好友
val old: RDD[((VertexId, VertexId), Int)] = graph.edges.map(e => ((e.srcId, e.dstId), e.attr))
val cur: RDD[((VertexId, VertexId), Int)] = graph.edges.map(e => ((e.dstId, e.srcId), e.attr))
old.join(cur)
.filter(t=>{
val a1: Int = t._2._1
val a2: Int = t._2._2
a1>=3 && a2>=3 && Math.abs(a1-a2)<=1
})
// ((源顶点(srcId),目标顶点(dstId)),(srcId至dstId的关系,dstId至srcId的关系))
.foreach(println)
----------------------------
((6,3),(4,4))
((1,6),(4,3))
((6,1),(3,4))
((5,2),(4,4))
----------------------------
案例三:合并重复边(限同分区内)
// 合并重复边:【同分区】内相同边(顶点ID顺序值都相同【如:(1,2),(1,3)】)合并
graph.partitionBy(PartitionStrategy.EdgePartition2D,1).groupEdges((a, b)=>{
val c: Int = a + b
println(s"$a + $b = $c")
c
}).triplets.foreach(println)
---------------------------
原有:
Edge(1L,6L,4),
Edge(1L,6L,4),
合并后:
Edge(1,6,8)
---------------------------