视频1：行列式的入门
原视频：线性代数！启动！从零开始到精通|第一集_哔哩哔哩_bilibili
一、二阶与三阶行列式
小学我们就接触过鸡兔同笼，这个问题让我们第一次接触到了方程组的思想。我们可以将它抽象成一个二元一次方程组，然后利用加减消元或带入消元就能很快的将方程组求出来。那如果是一个三元一次方程组呢？无非就是计算量大了些，但也能求。但如果是五元一次方程组呢？或者更高元的呢？那之前的方法就不太合适了。
所以为了解决这类方程组，数学家们发明了行列式。从而可以快速得出方程组的解。这里我们把方程组的系数抽出来，仍按照原来的位置，然后在两边加上两条竖线，得到的就是行列式。如下图👇
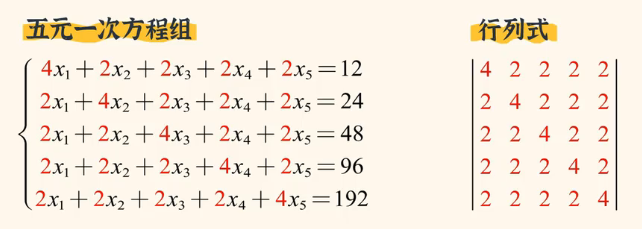
至此以后，这一类方程组的求解工作就变得非常简单了。这就是行列式出现的原因。
如果你想学号行列式，只需要搞懂4个问题：行列式的本质是什么、行列式是从哪来的、行列式是怎么定义的、行列式都有哪些性质
1、行列式的本质是什么
由上图👆，如果abcd都是常数的话，那么得到的最后结果也就是一个数字而已。这里你就已经知道了行列式的本质：行列式就是一个数而已。（很多考研的同学马上要上考场了，都还不知道行列式其实就是个数字）
所以这里我们可以粗略地下一个定义：行列式就是行数等于列数，边界有两条竖线的算式，最终的结果就是一个数字。
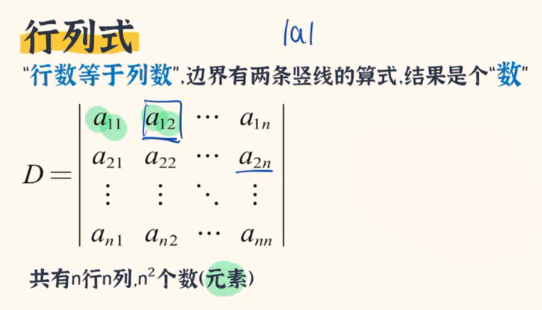
问：是否存在三行四列的行列式？
答：不存在。因为一开始我们就下了定义，行列式是行数等于列数的一个算式，而三行四列显然行数不等于列数，所以不行。
问：如果已知一个行列式内部不含参数，那么对这个行列式求导的结果是什么？
答：对行列式求导，结果为0。因为前面说过，行列式的结果就是一个具体的数，那也就是对这个数进行求导，结果当然是0
2、行列式是从哪来的
我们前面已经知道了行列式的本质，那么接下来我们看另一个问题：行列式是从哪来的。
我们现在来求解下图👇的二元一次方程组，我们将方程组转化成一种普适的形状，如果我们能将这个抽象化的方程组的解写成通项公式，那么面对所有的二元一次方程组我们都能将它的解给写出来。
现在，解虽然写出来了，但是有点太复杂了，这玩意儿要是当成通项公式背的话显然有难度。于是数学家们想，这个解有没有更简单的表达形式呢？
下面，我们来验证一下上面的推论是否正确👇
问：
问：三元一次方程组何时有唯一解？
答：当这个方程的未知数前面的系数组成的三阶行列式不等于0的时候，那么这个方程组就有唯一解。如下图👇
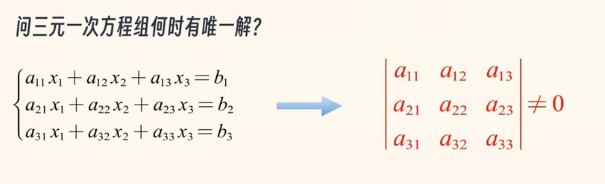
那么，三阶行列式如何求解呢？如下图👇
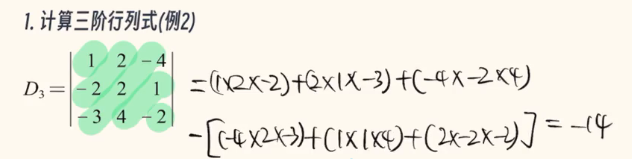
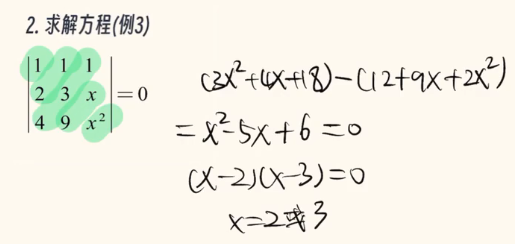
明白了低阶行列式怎么算之后，我们来简单回顾一下刚才所学的内容。
行列式的本质就看它的中文名，其实就是一个算式，算式的结果就是数字。
行列式的起源就看它的英文名，determinant，决定了这类方程组是否有唯一解。方程组的特点就是“方”，未知数个数等于方程个数。如果行列式不为0的话，就说明这个方程组它是有唯一解的。
那么到这里，第一节的内容我们就完全搞定了，接下来我们来介绍下一节的内容——全排列和对换的概念。👇
二、全排列和对换
1、全排列是啥？
其实，“全排列”这个名字起得不是很好，所以我们不妨用它的别名——n元排列
即：
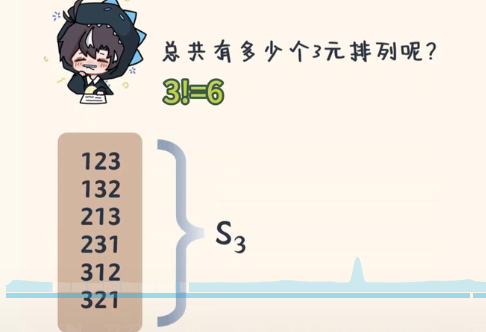
这样，我们就理解了全排列（即n元排列）是怎么一回事了。
2、逆序数是啥？
（1）逆序与逆序数
通过上图这样依次去看，然后连线的方式，逆序数可以很快地求出来。这么做的好处是不用走回头路，发现逆序数就连一条线，最后逆序数就等于线的个数。但是如果线太多了就容易乱啊。这一点不用担心，因为题目不会给我们一个很长的数让我们求它的逆序数的，一般最长也就5-6个数。
（2）奇偶排列
接下来我们介绍奇偶排列。这个概念其实也很简单，即：逆序数如果为奇数，那就是奇排列；如果逆序数为偶数，那就是偶排列。
那么为什么要介绍这个东西呢？其实在线性代数中，我们并不在意逆序数本身的大小，而是更在意它的奇偶性。比如两个n元排列，一个逆序数为1，另一个的逆序数为999，那么在我们眼里它们其实都叫奇排列就可以了，并不用在意它本身的大小。这个我们下节课再讲。
接下来，我们先把对换的概念讲明白。👇
（3）对换两数，奇偶改变
对换，顾名思义，就是在一组排列之中，把两个数进行交换的操作。那么只要发生了对换操作，逆序数的奇偶性就一定发生改变（即奇排列一定会变成偶排列，偶排列一定会变成奇排列）
（3-1）相邻对换
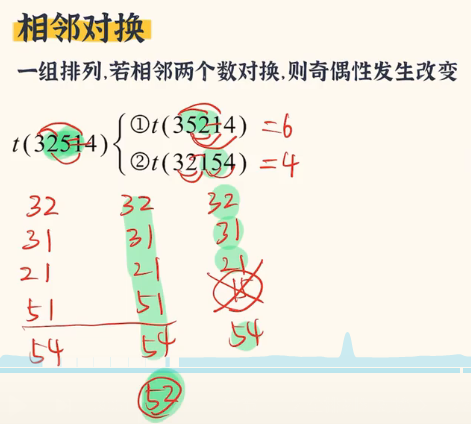
由上图👆，我们就可以观察出来，就是如果发生了相邻对换，其实大部分数的相对顺序并没有发生改变，改变的其实就看你交换的那两个数，如果它本来是顺序的话，你交换变成了逆序，那逆序数就加1，反之同理。所以这种加1减1的操作都会造成它的奇偶性发生改变。
下图是关于相邻对换的普适性表示。👇
对于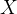
，以及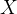，交换a和b对这些数都没有影响。但是对于ab来说，它俩的顺序发生了改变，所以逆序数要么加1，要么减1，而后果都是造成逆序数的奇偶性发生改变。
（3-2）任意对换
其实一个定理的证明往往是建立在一个更简单的定理之上的。那么根据我们上面学的“相邻对换”的性质，我们现在来研究“任意对换”对奇偶性的影响。
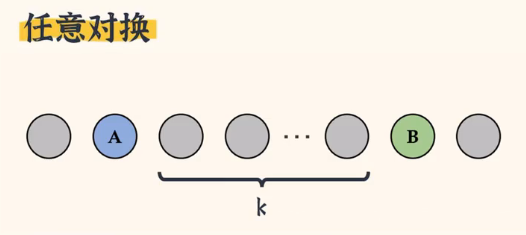
如上图👆，现在我们从一排数中任意选出A和B，它们之间隔了k个数。那如果我们想要直接交换A和B，想要判断逆序数是怎么变的其实比较困难。因为这和相邻对换不一样，因为它们中间夹了很多数。
那么我们可以这样，让A和右侧的数挨个交换，一共交换k次。如下图👇
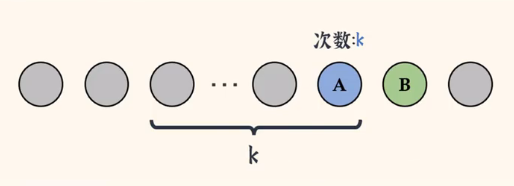
此时，A距离B仅剩一步之遥了。然后我们再让B去到A原先的位置。如下图👇
继续走，如下图👇
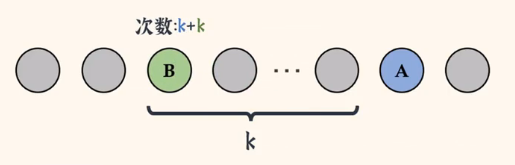
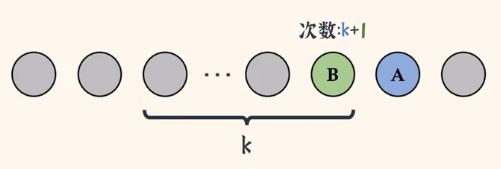
如上图👆，这时候，B只要再往前走一次，就到了A原先的位置。即：👇
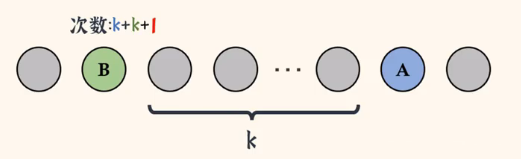
这时候，A和B就完成了一次任意对换。但实际上我们是通过次相邻对换达到的，并且其他数的位置并没有发生改变。显然
是个奇数，所以它的奇偶性一定发生了改变。
最后我们证明了：在一组排列中，只要两个数发生了对换（无论是相邻对换还是任意对换），那么这个排列的逆序数的奇偶性就一定发生改变（奇排列一定变成偶排列，偶排列一定变成奇排列）。
（3-3）逆序数的计算
